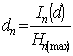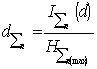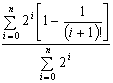THE GENERAL FORMULAS ON ENTROPY-INFORMATION ANALYSIS OF SELF-ORGANIZING HIERARCHICAL SYSTEMS
S.Sh.Kazhikenova, M.Kalikbergenova
In the article
the authors give the strict mathematical substantiation of all calculations and
the proof of several theorems to the general formulas on entropy-information analysis of self-organizing hierarchical systems. That
proves the high level of the given article. It can interest a reader as from
the point of view of its theoretical analysis of various technological
circuits, and also with its concern of the further development of entropy-information representations and display of any objects.
For accounting of a various
degree of unexpectedness (probability) of events K. Shannon has suggested to
use probabilities' function of entropy borrowed from statistical physics,
resulted as follows:
,
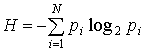where 
– is a probability of
detection of any homogeneous element of system in 
.
If 
is a probability of detection of a controllable
element then unexpectedness or uncertainty of this detection is equal to 
.
In our variant of estimation
this uncertainty will be expressed as:
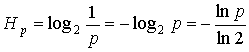. (1)
Before the publication of K.
Shannon's theory R.Hartly has suggested to define quantity of the information
under the formula:
, (2)
where 
, 
- number of levels, 
- length of a code of elements at each level of hierarchical system.
The theorem 1 Let 
- number of
elements of 
- level. 
- capacity of the information of a zero level of technological system.
Then the capacity of the
information of 
-level counting upon one element is expressed by the formula:
.
In the technological circuit
considered by us 
there is a sample
of set of elements - an element and not an element (in our case copper and all
other elements in aggregate) then the equation (2) will become:
.
Essentially important
advantage of an information estimation of quality of products or technological
operations is that a suggested parameter 
, as well as any entropy-information sizes, can be
added. The given property of additive is immanently inherent to entropy and
information and is a basis for expression of the law of preservation of their
sum. Hence, technological uncertainty of various operations within the limits
of the unified circuit can be expressed by a system parameter of uncertainty:
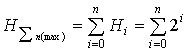, Bit/el.
The theorem 2 Information capacity of hierarchical system and n- level are defined by equality:
, 
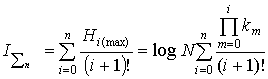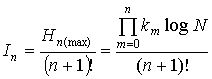, (3)
where 
- greatest possible
entropy of a system.
The determined component of
the information 
on the basis of the
theorem 2 is defined by equality:
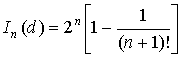Bit/el.
The system determined
component 
is equal:
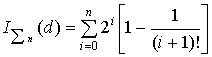Bit/el.
Having defined degrees of
determination and ineradicable stochasticity at each level of technological
system under formulas:
, 
,
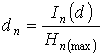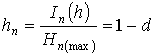let's analyze the received results of the carried out calculations which
are submitted in table 1.
Table 1 -
Settlement information-entropy characteristics of hierarchical system for 
, 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1,0 |
0 |
0 |
1,0 |
0 |
|
1 |
1,0000 |
2,0 |
0,5000 |
1,0000 |
3,0 |
0,3333 |
|
2 |
3,3333 |
4,0 |
0,8333 |
4,3333 |
7,0 |
0,6190 |
|
3 |
7,6667 |
8,0 |
0,9583 |
12,0000 |
15,0 |
0,8000 |
|
4 |
15,8667 |
16,0 |
0,9917 |
27,8667 |
31,0 |
0,8989 |
|
5 |
31,9556 |
32,0 |
0,9986 |
59,8222 |
63,0 |
0,9496 |
|
6 |
63,9873 |
64,0 |
0,9998 |
123,8095 |
127,0 |
0,9749 |
|
7 |
127,9968 |
128,0 |
1,0 |
251,8063 |
255,0 |
0,9875 |
|
8 |
255,9993 |
256,0 |
1,0 |
507,8056 |
511,0 |
0,9937 |
|
9 |
511,9999 |
512,0 |
1,0 |
1019,8055 |
1023,0 |
0,9969 |
|
10 |
1024,0000 |
1024,0 |
1,0 |
2043,8055 |
2047,0 |
0,9984 |
|
11 |
2048,0000 |
2048,0 |
1,0 |
4091,8055 |
4095,0 |
0,9992 |
|
12 |
4096,0000 |
4096,0 |
1,0 |
8187,8055 |
8191,0 |
0,9996 |
|
13 |
8192,0000 |
8192,0 |
1,0 |
16379,8055 |
16383,0 |
0,9998 |
|
14 |
16384,0000 |
16384,0 |
1,0 |
32763,8055 |
32767,0 |
0,9999 |
|
15 |
32768,0000 |
32768,0 |
1,0 |
65531,8055 |
65535,0 |
1,0 |
The size 
in this case does
not influence the solution of a problem as it is reduced at calculation of
level determinations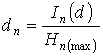 
and system
determination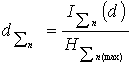 
.
Influence of length of a code 
that is elements of system
(target component and the basic impurity) can be revealed in the further
researches. As a whole the improvement of quality of a product in process of
its technological processing correlates with dynamics of growth of the
determined component in abstract hierarchical system that proves the expediency
of the further entropy-information analysis of similar
systems. It can interest a reader as from the point of view of its theoretical
analysis of various technological circuits, and also with its concern of the
further development of entropy-information representations and
display of any objects.