Технические науки/2. Механика.

к.ф.-м.н Нуримбетов. А.У.

МАИ – Московский авиационный институт (НИУ), Россия

к.т.н. Джунисбеков М.Ш.

Таразский государственный университет им. М.Х. Дулати

Тараз, Казахстан

Продольная колебания композиционного стержня

прямоугольного сечения

На примере стержня исследуется влияние взаимодействия компонентов композиции на свободные колебания армированных тел.

Для решения задачи колебания стержней необходимо связать компоненты кинематических характеристик деформации стержня с силовыми. Когда принят определенный вид функциональных зависимостей для компонент перемещений U,V,W, методами теории упругости можно получить зависимости для деформаций, а затем и напряжений в стержне. Зная напряжения, всегда можно перейти к компонентам главных вектора и момента внутренних сил в стержне. Теория деформаций закрученных стержней произвольного профиля, являющуюся естественным обобщением теории Кирхгофа-Клебша на закрученные стержни, в дальнейшем нуждается в сопоставление ее результатов с некоторыми простыми частными точными решениями и всесторонняя экспериментальная проверка. Частный и практически наиболее важный случай этой теории, относящийся к стержням удлиненного профиля, является продольная и поперечная колебания стержней прямоугольного сечения.

Продольные колебания стержня. На практике продольные колебания возникают чаще всего тогда, когда стержень предварительно немного растягивается или, наоборот, сжимается, а затем предоставляется самому себе. В этом случае в нем возникают свободные продольные колебания.

Направим ось z по оси стержня (рис. 1); в состоянии покоя концы стержня имеют соответственно z=0, z=l. Рассмотрим сечение pqrs, z - его координата в состоянии покоя.

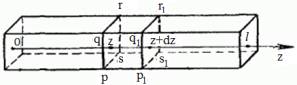
Рис. 1.

Смещение этого сечения в любой момент времени t будет характеризоваться функцией w(z,t) и для ее отыскания можно получить дифференциальное уравнение в виде [1]:

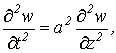(1)

где a²=/ρ, с₃₃ – параметр упругости сечения, r - объемная плотность стержня.

Итак, задача о свободных продольных колебаниях стержня, закрепленного на одном конце, возникающих благодаря начальному сжатию или растяжению, определяется из уравнения

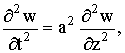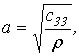где (2)

с начальными условиями

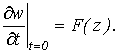(3)

и краевыми условиями

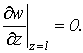(4)

Для решения задачи используется метод Фурье и можно пoлучит искомое решение в виде [1]:

(5)

(6)

1. Колебания стержня со свободным концом при действий растягивающей силы. Пусть однородный стержень плотности r и длины l, закрепленный в точке z=0 растянут силой Р, приложенной к свободному концу. В момент времени t=0 действие силы мгновенно прекращается, после чего стержень предоставлен самому себе. Найдем возникающие продольные колебания стержня.

Сила Р, действующая на стержень в начальный момент, такова, что применим закон Гука, и найдем начальное смещение точек стержня  Так как в каждом сечении сила натяжения Т постоянна и равна Р, то 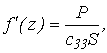где с₃₃ - модуль упругости, S - площадь поперечного сечения. Интегрируя и учитывая, что f(0)=0 (стержень при z=0 закреплен), получим 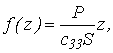т. е. смещение любого сечения в начальный момент пропорционально z. Так как начальные скорости равны нулю, то F(z)=0 и все  b_k  обращаются в нуль. Найдем теперь по формуле (7) коэффициенты a_k

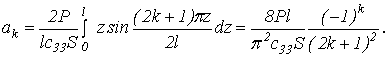(7)

Подставляя выражения для a_k  в формулу (5), получим функцию  w(z,t), описывающую продольные колебания стержня:

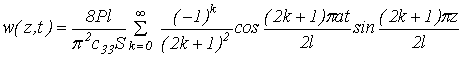(8)

где 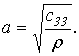Наибольшее смещение конца стержня от положения равновесия будет при 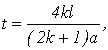 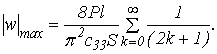Так как при z=l то на свободном конце стержня все гармоники имеют пучность. Ясно, что в закрепленном конце всегда будет узел. Первая гармоника имеет частоту 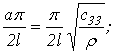 это есть основная частота колебаний стержня. Частоты остальных гармоник будут получаться при умножении основной частоты на последовательные нечетные числа.

Найдем возникающие колебания стержня, если cтержень растянут силой Р=590 Н., приложенной к свободному его концу. Была проведена серия численных экспериментов с образцами прямоугольного сечения из алюминия (таблица 1) и из углепластика армированный волокнами под углом 60⁰ по длине стержня. Рассматривается образцы шириной l=62 mm, толщиной h=4,7 mm и длиной 120 mm. (рис.1).

Таблица. Свойства материала.

№	1	2	3	4	5	6	7	8	9	10
Свойства материала	Е1, кг/mm^2	Е2,кг/mm^2	Е3,кг/mm^2				G12,кг/mm^2	G13,кг/mm^2	G23,кг/mm^2	, кг/mm^3
Aлюминий	7000	7000	7000	0.34	0.34	0.34	2700	2700	2700	2.7E-09
Углепластик	15700	15700	112500	0.3	0.48	0.3	3300	5300	5300	1.67E-09

Наибольшее смещение конца стержня от положения равновесия будет при достижения значения (8)

На рис.2 приведена изменения перемещений W(t,z) по длине алюминиевого стержня при различных значениях t. Расчеты по времени продолжается до достижения значения

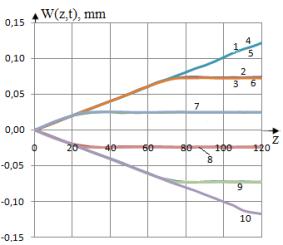
Рис.2. Изменения перемещений W(t,z) по длине стержня при различных значениях t (1 - t=2.40E-05, 2 – 4.81E-05, 3 – 7.21E-05, 4 – 9.61E-05, 5 – 1.20E-04, 6 – 1.44E-04, 7 – 1.68E-04, 8 – 1.92E-04, 9 – 2.16E-04, 10 – 2.40E-04).

Как видно из расчетов значения перемещения W(z,t) достигает наибольшего значения по абсолютной величине в момент времени t=2.40E-05, t=9.61E-05, t=1.20E-04, t=2.40E-04. С увеличением времени значения перемещении стабилизируется (линии 7,8) и достигает своего минимума. Далее значения перемещения от стабильного значения (линия 7,8) переходит к линейному росту (линия 1,4,5 и 10) и достигает своего наибольшего значения (линия 10, 5). Значение перемещений в период времени достигает своего максимума дважды (линии 1,5), а затем за такой период времени убывает (линии 6,7,8,9) и достигает своего максимума (линии 10). Таким образом период повторения наибольшего значения перемещении будет отрезок времени

На рис.3 приведена изменения перемещений W(t,z) по длине стержня из углепластика, армированные волокнами под углом 60⁰ по длине стержня при различных значениях t. Расчеты по времени продолжается до достижения значения t=1,22E-04.

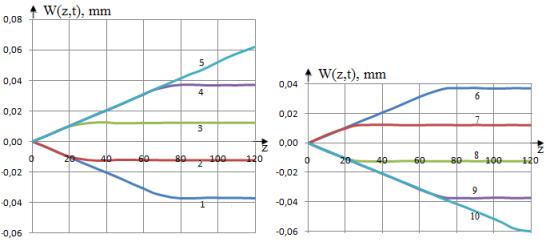
Рис.3. Изменения перемещений W(t,z) по длине стержня при различных значениях t (1 - t=1,22E-05, 2 - 2,44E-05, 3 - 3,67E-05, 4 - 4,89E-05, 5 - 6,11E-05, 6 - 7,33E-05, 7 - 8,56E-05, 8 - 9,78E-05, 9 - 1,10E-04, 10 - 1,22E-04).

Как видно из расчетов значения перемещения W(z,t) в момент времени t=0.162E-04 достигает наибольшего значения по абсолютной величине в момент времени t=0.325E-04 и t=0.649E-04. С увеличением времени значения перемещении стабилизируется (линии 2,3,4). Далее значения перемещения от стабильного значения (линия 7,8 и 2,3) переходит к линейному росту (линия 10 и 5) и достигает своего наибольшего значения (линия 5, 10). Изменение перемещений по длине стержня с увеличением времени из углепластика по сравнению стержня из алюминия не симметрично и по абсолютной величине меньше в два раза. Это связана с углом армирования волокна на 60⁰ по длине стержня. Таким образом период повторения наибольшего значения перемещении увеличивается два раза, т.е.

2 Колебания стержня со свободным концом при действий удара в продольном направлений. Пусть стержень выводится из состояния равновесия ударом по его свободному концу в продольном направлении. Найдем возникающие колебания стержня, если импульс, сообщенный стержню при ударе, равен . В этом случае наибольшую трудность представляет формулировка начальных условий. Сообщение стержню ударного импульса приводит к тому, что точки его свободного конца получают начальные скорости. Удар предполагается мгновенным, поэтому начальные скорости, строго говоря, должны получать только те точки стержня, которые лежат в сечении z=l. Поэтому мы выделяем малый участок стержня  и считаем, что все его точки получили в результате удара одну и ту же скорость v₀. Масса выделенного участка равна ρSε, где r - плотность стержня и S - площадь поперечного сечения. Приравнивая изменение количества  движения импульсу силы, получим откуда Функции f(z), F(z) определяющие начальное состояние стержня, будут равны: f(z)=0, 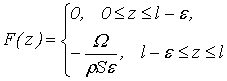(знак минус берется потому, что скорость v₀ направлена в отрицательную сторону оси 0z). Коэффициенты, входящие в общую формулу (5), находим по формулам (6): 

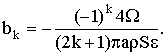
Подставляя выражения для  в формулу (5), окончательно получим

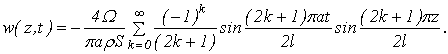(9)

Период колебания  Смещение w(l,t) равно нулю при  . Наибольшее смещение конца стержня от положения равновесия будет при 

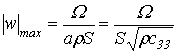. (10)

Найдем возникающие колебания стержня, если импульс, сообщенный стержню при ударе, равен =59 кг мм/с. Была проведена серия численных экспериментов с закрученными образцами прямоугольного сечения из алюминия и углепластика (таблица 1). Рассматривается образцы шириной l=62 mm, толщиной h=4,7 mm и длиной 120 mm . (рис.1).

На рис.4 приведена изменения перемещений W(t,z) по длине стержня при различных значениях t. Расчеты по времени продолжается до достижения значения . Максимальное значение перемещений W(t,z) (9) достигает своего значения при t=1.92 10E-4 (рис.4– линия 2,3,7,8) и с увеличением t знаечения W(t,z) уменьшается (рис.4 – линия 1,4,6,9), и затухает (рис.4 – линия 5,10).

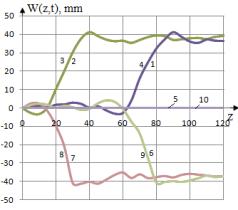
Рис.4. Изменения перемещений W(t,z) по длине стержня при различных значениях t (1 - t=2.40E-05, 2 – 4.81E-05, 3 – 7.21E-05, 4 – 9.61E-05, 5 – 1.20E-04, 6 – 1.44E-04, 7 – 1.68E-04, 8 – 1.92E-04, 9 – 2.16E-04, 10 – 2.40E-04).

На рис.5 приведена изменения перемещений W(t,z) по длине углепластикового стержня при различных значениях t. Расчеты по времени продолжается до достижения значения . Максимальное значение перемещений W(t,z) (10) достигает своего значения при t=4.81E-05, t= 7.21E-05, t=1.68E-04, t=1.92E-04 (рис.5, 3– линия 7,8) и с увеличением t значения W(t,z) уменьшается и затухает (рис.5 – линия 4,5 и 9,10). Значения линии 2 и 3 (7,8), а также 1 и 4 (6,9) совпадают, что определяет период повторения значения перемещении W(z,t) по времени. Значение продольного перемещения стержня из углепластика по абсолютной величине меньше значения стержня из алюминия на 10% из за угла армирования волокон углепластика на 60⁰ по длине стержня.

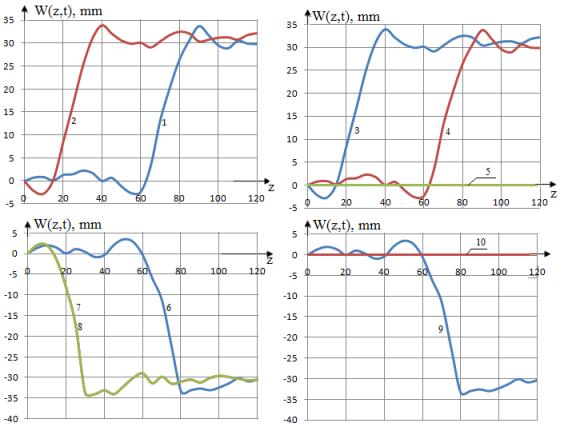
Рис.5. Изменения перемещений W(t,z) по длине стержня из углепластика при различных значениях t (1 - t=1,22E-05, 2 - 2,44E-05, 3 - 3,67E-05, 4 - 4,89E-05, 5 - 6,11E-05, 6 - 7,33E-05, 7 - 8,56E-05, 8 - 9,78E-05, 9 - 1,10E-04, 10 - 1,22E-04).

3. Колебания стержня, когда свободному концу приложена сила Q, действующая вдоль стержня. Пусть стержень длины  l конец которo-го z=0 закреплен, находится в состоянии покоя. В момент t=0 к его свободному концу приложена сила Q, действующая вдоль стержня. В этом случае решения уравнения свободных колебаний стержня (5) с начальными условиями

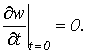(11)

и краевыми условиями

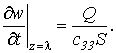(12)

описываются функцией

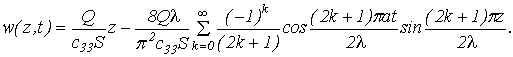(13)

Найдем возникающие колебания стержня, если свободному концу приложена сила Q=590 Н., действующая вдоль стержня. Была проведена серия численных экспериментов с образцами прямоугольного сечения из алюминия и углепластика (таблица 1). Рассматривается образцы шириной l=62 mm, толщиной h=4,7 mm и длиной 120 mm . (рис.1).

На рис.6 приведена изменения перемещений W(t,z) по длине стержня при различных значениях t. Расчеты по времени продолжается до достижения значения

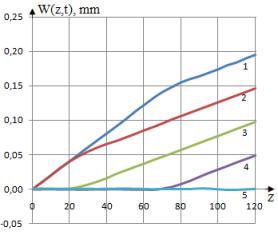
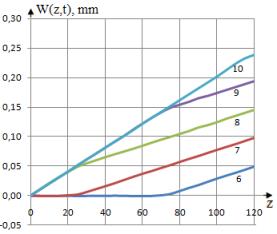
Рис.6. Изменения перемещений W(t,z) по длине стержня из алюминия при различных значениях t (1 - t=2.40E-05, 2 – 4.81E-05, 3 – 7.21E-05, 4 – 9.61E-05, 5 – 1.20E-04, 6 – 1.44E-04, 7 – 1.68E-04, 8 – 1.92E-04, 9 – 2.16E-04, 10 – 2.40E-04).

Как видно из расчетов (рис.6) значения перемещения W(z,t) в промежуток времени t=1.2E-04 (линия 5) равно нулю и достигает наибольшего значения по абсолютной величине в момент времени t=2.4E-04 (линия 10). С увеличением времени значения перемещении меняется линейно по длине стержня (линии 2,3) и достигает своего минимума (линия 5). Далее значения перемещения от нулевого значения (линия 5) переходит к линейному росту (линия 7,8) и достигает своего наибольшего значения (линия 10). Таким образом период повторения наибольшего значения перемещении будет отрезок времени

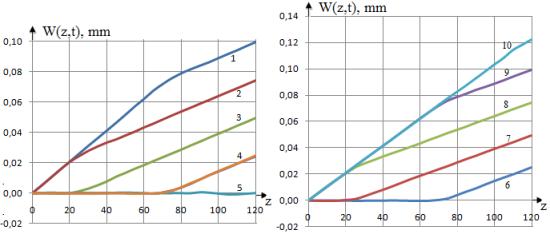
Рис.7. Изменения перемещений W(t,z) по длине стержня из углепластика с волокнами уложенных под углом 60⁰ при различных значениях t (1 - t=1,22E-05, 2 - 2,44E-05, 3 - 3,67E-05, 4 - 4,89E-05, 5 - 6,11E-05, 6 - 7,33E-05, 7 - 8,56E-05, 8 - 9,78E-05, 9 - 1,10E-04, 10 - 1,22E-04).

Как видно из расчетов (рис.7) значения перемещения W(z,t) стержня из углепластика достигает наименьшего значения в момент времени t=0.611E-05. Далее значения перемещения от нулевого значения (линия 5) переходит к линейному росту (линия 7-10) и достигает своего наибольшего значения (линия 10). Значение продольного перемещения стержня из углепластика по абсолютной величине меньше значения стержня из алюминия в два раза. Это связана свойствами углепластика армированного под углом 60⁰ по длине стержня.

Литература:

1. Нуримбетов А.У., Джунисбеков М.Ш. Колебания стержня прямоугольного сечения. //Тр. VIII межд. науч.практ.конф. «Инженерные системы – 2015». Москва: РУДН. -2015.-с. 97-102.