Технические науки/ Авиация и космонавтика

Nickolay Zosimovych

National Aviation University, Kyiv, Ukraine

SIMULATION OF THE INTEGRATED ONBOARD SYSTEM FOR A COMMERCIAL LAUNCH VEHICLE

In the article has been chosen and modeled integrated guidance system of a commercial launch vehicle with application of GPS technologies. Under researching was developed process of simulation of the dynamics of the spacecraft constellation, providing the process of functioning integrated navigation system of the launch vehicle by using object-oriented approach.

Keywords: Guidance, Launch Vehicle (LV), Onboard Integrated Control System (OICS), Inertial Navigation System (INS), Global Positioning System (GSP), gyro, satellite, constellation, Gravitational Potential of the Earth (GPE), Sun, Moon, pseudorange, pseudovelocity, object-oriented approach (OOA).

I. Introduction. In this study we shall consider a concept of integrated onboard systems for launch vehicles in the context of the current task, and provide mathematical models of all its elements for different variants of their structure and composition.

Integrated onboard guidance and navigation systems used in launch vehicles allow applying modern information technologies most appropriately to ensure the required quality (accuracy and reliability) of navigation [1-3]. The analysis shows that the onboard integrated control systems (OICS) have a number of features, main among them being unification of respective functional groups on the level of technical solutions [4, 5]. For example, all processor sections of a computer system are the same, irrespective of the problem they solve: navigation, guidance or stabilization. This fact makes away with one of the main disadvantages of the traditional (composite) on-board control system – excess range of schematic and technical solutions [6].

Unification of schematic and technical solutions by minimizing their number and the number of hardware components results in higher system reliability, reduction in the number of control and of technological equipment, cutting of development time and, ultimately, reduction in the cost of both the system as a whole, and the process of its design [2].

It is known that the algorithm of inertial navigation system is based upon integration of acceleration values of the launch vehicle sent by integrating accelerometers and reconstruction based upon calculation of the apparent way of its full position and the velocity in the coordinate system used to solve the navigation task by taking into account accelerations caused by the gravitational influence of the Earth [3, 4, 7, 8].

II. Problem setting. The process of conceptual design of the onboard integrated system for a commercial launch vehicle includes in particular synthesis of navigation and control algorithms. In its turn, the synthesis may be successfully implemented only if there are appropriate adequate models of motion of the object, permanent (predetermined) elements of control and navigation system (control actuators, gyroplatform or SINS, GPS receiver, etc.), as well as models of steering and disturbance forces and moments influencing the launch vehicle in flight.

It is obvious, that viability and efficiency of the synthesized algorithms and the adequacy of the respective models can be described in details in the present research only by imitation mathematical simulation of the process of controlled motion of the launch vehicle taking into account the whole range of steering forces and moments.

Such simulation suggests creating sets of motion and disturbance models. The first of such sets shall make a so-called model of “external environment”, and the components making the model are most explicit and exact. This refers primarily to simulation of the center of mass of LV, as well as to disturbance models. All the named models have already been described earlier [3, 8]. Here we shall only remind that in the process of creation of a “real” trajectory of LV chance factors such as divergence of initial launch conditions, error in the assembly of the stages of the launch vehicle (turn and misalignment of stages in reference to their target position), thrust deviation from the vector rated in size and directionally, variations in atmospheric density, drift and trend of output signals of gyroblocks and accelerometers, errors in tailoring of pseudo ranges and pseudo velocities owing to onboard clock bias and zenithal errors (tropospheric and ionospheric refraction), errors of actuating mechanisms will be taken into consideration as well. Non-sphericity and anomalies of Earth's gravitational field were considered as a determining disturbing influence.

We shall point out that such formulation of a guidance task is naturally simplified as much as possible, and doesn’t allow, in particular, to study the process of injecting a payload into the Earth orbit, because this process supposes manoever of the final stage, and consequently solving on board a respective boundary task in one form or another. But, as it has been many times emphasized [1, 3, 4, 7, 8], the purpose of the present research is to formulate efficient and precise navigation algorithms, based on the use of SINS and the GPS - receiver. In connection with the foregoing, it is obvious that high precision solution of a navigation task will allow to implement manoevers needed to launch a payload, all other conditions being equal.

III. Results and Discussion. Statement of a simulation task may be illustrated using a functional scheme [8], which suggests creation of an instrument, namely a program complex designed to implement tasks and objectives of research.

The most appropriate and suitable for the creation of such a complex is object-oriented approach (OOA). This approach makes it possible to develop a flexible and extensible Methodological Software of the required level of complexity, allowing to use hierarchical structures of inherited classes in the form of appropriate libraries, and to ensure security of stored data [9].

It must be noted that while using OOA, we have to determine the so-called processes and the structure of the corresponding hierarchy of these classes [9]. This type of research is very poorly formalized, but, nevertheless, based on existing experience we can make the following recommendations for development of an object- oriented scheme of software and mathware:

1. All the material objects of research, such as aircraft, control systems, power meters, etc., which are the systems with a finite number of inputs and outputs must be a "black box" with a number of properties, but with a hidden mechanism of functioning.

2. It is advisable to start building up a hierarchical chain of such classes with the most general, abstract class, where only the most general fields, typical for the whole intended chain, are identified, and where methods are declared as virtual and abstract ones. In other words, in such classes only field structures and template methods are declared, and the method bodies themselves are absent. This requires overlapping them in descendant classes.

3. If complex algorithms requiring a large number of settings and additional procedures are used during the simulation, it is necessary to build up libraries for the correspondent classes that shall implement the mentioned algorithms. In such a case, the method which specifies the initial mathematical problem must be declared abstract to further overlap in the descendant within the present project (for example, the function of calculation of the right sides of the system of ordinary differential equations).

4. It is advisable that auxiliary procedures and simple algorithms should take the forms of individual modules without ascribing them to any class in order to simplify the overall structure and, as noted above, to improve the performance of the program. For example, the best thing is to collect the functions and procedures of matrix algebra, algebra of complex numbers, quaternions, tensors, etc. in separate modules, having previously described respective types (matrix, complex number, quaternion, tensor etc.).

5. If the studied processes are characterized by nesting, i.e. one process is connected directly or indirectly with several others, the class that implements this process must provide the appropriate field for the object from the class, which implements the nesting process. It should be noted that such nested objects are to be created from the outside, i.e. in the calling program with transmission of the created objects into the addressed classes. It is necessary to ensure that the different classes use only one instance of this class, and access to its data is coordinated. Thus, during the initialization of the whole structure, most independent simple objects must be created first, and thereafter complex composite objects are to be made.

Thus, considering the above, we may present the architecture of a software complex that implements the functional diagram [8]. This architecture is shown in Fig. 1. Because when creating a software system, you should be guided by the requirements in respect of the efficient use of computing resources, as well as by the requirements regarding accuracy and speed of calculations.

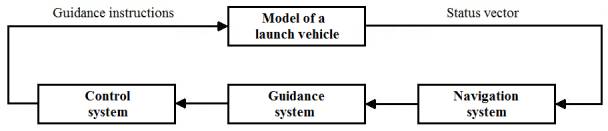
Fig. 1. Architecture of a software complex

Let’s consider each of the elements of the functional diagram in order to determine the composition and functional purpose of the classes, which determine object structure of software and mathware in compliance with OOA.

The LV Model Block describes the dynamics of LV (as the center of mass (CM) and angular motion) influenced by forces and moments conditioned by the environment and deflection of controls. In order to determine basic classes and the corresponding chains of descendant classes implementing the element under consideration, we shall specify the required models and algorithms implementing the process of simulation of the LV dynamics with indication of the required initial data.

In its core, the problem in question is the task of integrating the system of ordinary differential equations (ODE) of the first order.

Thus, in the context of software implementation, the block contains two classes: a class that implements the numerical method of integration of ODE systems, and the class describing a model of forces and moments of uncontrolled motion of the CM and the angular motion of the LV.

Let’s consider the chain of classes implementing the library of methods of numerical integration of ODE systems (Fig. 2).

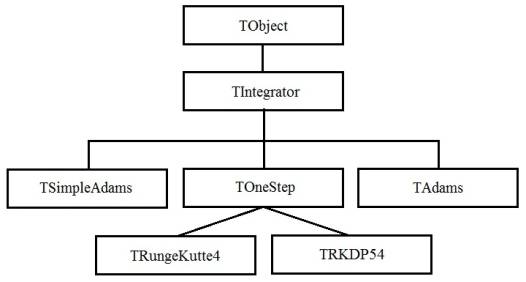
Fig. 2. Library of the methods of numerical integration of the systems of ordinary differential equations

The library contains the following methods:

· Runge-Kutte methode;

· the nested Dormand-Prince method;

· Adam-Bashforth-Moulton predictor-corrector method.

All the methods accept the nested one, have a constant integration step and lacks evaluation of local error at each step. The predictor-corrector method is an iterative one, and completion of iterations is determined either upon achievement of a given accuracy of residual error in the two last solutions, or upon achievement of a specified number of iterations.

To solve the problem of simulation of the LV dynamics we will use the nested Dormand-Prince method of the Runge-Kutte family [10], and to solve the basic navigation equation for INS, the predictor-corrector method will be used.

The full vector of the dynamic system status includes components of position, velocity of the LV in the ideal navigation coordinate system INCS, the quaternion components and output signals from drives of control motors of the LV. At the same time, we shall note that due to the discrete nature of the control loop (frequency 64 Hz), control signals are assumed to be constant during one cycle of the system controlling the operation of control engines.

The numerical integration methods themselves are described in detail in [74], and the peculiarities of the implementation of these methods regarding salvation of aerospace tasks are described in [11].

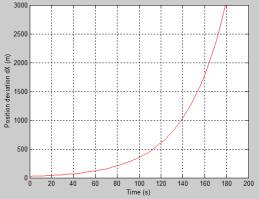
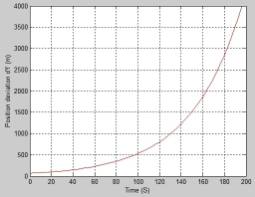
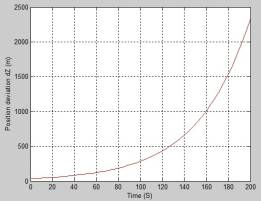
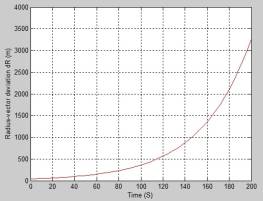
Simulation Results and their Analysis. The Fig. 3-4 show average to implementation deviations of the position and velocity of the LV in the ideal navigation coordinate system estimated with application of the strapdown inertial navigation system (SINS) [12, 13].

Fig. 3. Deviation of the X,Y-coordinates

Fig. 4. Deviations of the Z-coordinate and the radius-vector R

IV. Conclusions.

1. Offered a concept of the integrated navigation system for the commercial launch vehicle using GPS technologies.

2. Developed a system of models and algorithms providing both modeling of the process of functioning of the integrated navigation system and function simulation of the onboard navigation system of the launch vehicle itself.

3. The system includes:

1) a model of controlled motion of the center of mass within 3 stages of the launch vehicle and relative to the center of mass, taking into account non-centrality of the gravitational field, variations in the density of the atmosphere, wind gusts, thrust distribution, assembly errors and thrust errors;

2) algorithms for solving navigation tasks using GSP, OINS and GPS data;

4. The number of errors in determining position and velocity of a launch vehicle reduce in rigidly bound systems using a strapdown inertial navigation system and a GPS receiver (error along the radius vector is m and the absolute velocity is

References

1. Nickolay Zosimovych, Anatoly Voytsytskyy. Design objectives for a commercial launch vehicle with integrated guidance system. Novus International Journal of Engineering&Technology, Vol. 3, No 4, 2014, PP.7-28.

2. Nickolay Zosimovych, Anatoly Voytsytskyy. Disturbed Motion of the Launch Vehicle with Integrated GPS/INS Navigation Systems. "Бъдещите изследвания – 2014" Proc. X International Scientific and Practical Conference, Sofia, 17-25 February, Vol. 49. Technologies. Physics, Sofia: Бял ГРАД-БГ, 2014, PP. 3-9.

3. Nickolay Zosimovych. Integrated Guidance System of a Commercial Launch Vehicle. "Modern European Science – 2014" Proc. X International Scientific and Practical Conference, Sheffield, 30 June – 7 July, 2014, Volume 18. Technical sciences, Science and education LTD, 2014. - PP. 10-22. ISSN 978-966-8736-05-6, Registrated Number: 08878342.

4. Zosimovych Nickolay. Selecting Design Objectives for an Integrated Guidance System of a Commercial Launch Vehicle with Application of GPS Technologies. The Open Aerospace Engineering Journal, 2013, Vol. 6, PP. 6-19.

5. Jiann-Woei Jang, Abran Alaniz, Robert Hall, Nazareth Bedrossian, Charles Hall, Mark Jackson. Design of Launch Vehicle Flight Control Systems Using Ascent Vehicle Stability Analysis Tool. AIAA Guidance, Navigation, and Control Conference, 08-11 August 2011, Portland, Oregon, USA, AIAA 2011-6652.

6. Nail F. Palumbo, Brian E. Reardon, and Ross A. Blawkamp. Integrated Guidance and Control for Homing Missiles. Johns Hopkins APL Technikal Digest, Vol. 25, №2, 2004, pp. 121-139.

7. Nickolay Zosimovych. Modeling the Integrated Guidance System of a Commercial Launch Vehicle, International Refereed Journal of Engineering and Science (IRJES), Volume 3, Issue 6, June 2014, PP. 39-54.

8. Nickolay Zosimovych, Functional Simulation of the Integrated Onboard System for a Commercial Launch Vehicle, International Refereed Journal of Engineering and Science (IRJES), Volume 3, Issue 11, November, 2014, PP.92-106, ISSN (Online) 2319-183X.

9. Шлеер С., Меллор С. Объектно-ориентированный анализ: моделирование мира в состояниях: Пер. с англ. — Киев: Диалектика, 1993, 240 с: ил.

10. Alfio Quarteroni, Alberto Valli. Numerical Approximation of partial Differential Equations. Springler Series in Computational Mathematics, 1991.

11. Кудряшов С.В. Основы статистической динамики комплексных информационных систем, М.: МАИ, 2003.

12. Nickolay Zosimovych, A Model of Dynamics of a Constellation of Navigation Satellites. Nauka i studia, № 3 (134), 2015, PP. 51-58, ISSN 1561-6894.

13. Nickolay Zosimovych, Model of Inertial Navigation System with Integration Schemes for a Commercial Launch Vehicle. International Journal of Engineering Technology&Advanced Engineering (IJETAE), Vol. 5, Issue 2, February, 2015, PP. 479-485, ISSN 2250-2459, ISO 9001:2008 Certified Journal.