К. ф.-м. н. Касьянюк В.С.
КНУ им. Т. Шевченко, Киев, Украина
Об
использовании метода парето-оптимальной интерполяции линейных функционалов в
задаче спектрального оценивания
Рассматривается задача восстановления
функции ![]() на
на ![]() по ее коэффициентам
Фурье
по ее коэффициентам
Фурье
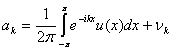 ,
, ![]() , (1)
, (1)
известным со случайными погрешностями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , * - символ транспонирования и комплексного сопряжения.
Традиционно [1] функцию
, * - символ транспонирования и комплексного сопряжения.
Традиционно [1] функцию ![]() восстанавливают как
восстанавливают как ![]() -ю частичную сумму ряда Фурье с коэффициентами
-ю частичную сумму ряда Фурье с коэффициентами ![]()
![]() ,
, ![]() .
.
При этом ![]() представляет собой
некоторый линейный функционал, который можно интерпретировать как выход
функции
представляет собой
некоторый линейный функционал, который можно интерпретировать как выход
функции ![]() с линейного прибора с
некоторой аппаратной функцией. В самом деле,
с линейного прибора с
некоторой аппаратной функцией. В самом деле,
![]()
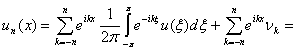
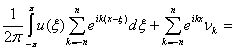
![]()
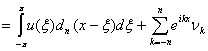 ,
, ![]() (2)
(2)
где
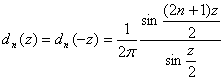 ,
, ![]() (3)
(3)
обозначает функцию Дирихле.
Поскольку аппаратная функция (3) при
небольших ![]() имеет значительные
боковые лепестки и достаточно широкий главный лепесток, возникает явление
Гиббса, существенно искажающее
имеет значительные
боковые лепестки и достаточно широкий главный лепесток, возникает явление
Гиббса, существенно искажающее ![]() как оценку
как оценку ![]() . Кроме того, задача суммирования рядов Фурье с погрешностями
в данных относится к классу некорректных задач
[2]. В данном случае оценка (2)
содержит шумовой фон
. Кроме того, задача суммирования рядов Фурье с погрешностями
в данных относится к классу некорректных задач
[2]. В данном случае оценка (2)
содержит шумовой фон ![]() , уровень которого определяется величиной
, уровень которого определяется величиной ![]() , неубывающий с ростом
, неубывающий с ростом ![]() . Более того, если все
. Более того, если все ![]() , то как бы мало ни было
, то как бы мало ни было
![]() ,
, ![]() при
при ![]() . Поэтому для качественного восстановления функции
. Поэтому для качественного восстановления функции ![]() по конечному числу
коэффициентов Фурье (1) возникает проблема подавления и артефактов, возникающих из-за
ограниченности
по конечному числу
коэффициентов Фурье (1) возникает проблема подавления и артефактов, возникающих из-за
ограниченности ![]() , и шумового фона,
порожденного случайными погрешностями в данных..
, и шумового фона,
порожденного случайными погрешностями в данных..![]()
В качестве оценки, удовлетворяющей этим
условиям, предлагается принять результат редукции коэффициентов Фурье к выходу
функции ![]() с линейного прибора
с линейного прибора 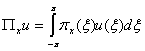 с «хорошей» аппаратной функцией
с «хорошей» аппаратной функцией ![]() , лишенной
недостатков функции Дирихле. При этом следует учитывать влияние шумовой
компоненты и позаботиться об уменьшении уровня шумового фона искомой оценки.
Этой цели отвечает парето-оптимальная интерполянта [3] функционала
, лишенной
недостатков функции Дирихле. При этом следует учитывать влияние шумовой
компоненты и позаботиться об уменьшении уровня шумового фона искомой оценки.
Этой цели отвечает парето-оптимальная интерполянта [3] функционала ![]() по значениям функционалов (1), содержащим случайные
погрешности
по значениям функционалов (1), содержащим случайные
погрешности ![]() , которая строится в ходе решения двукритериальной задачи
минимизации по Парето шумового фона искомой интерполянты и ее операторной
невязки, характеризующей смещение.
, которая строится в ходе решения двукритериальной задачи
минимизации по Парето шумового фона искомой интерполянты и ее операторной
невязки, характеризующей смещение.
Парето-оптимальная интерполянта
функционала ![]() по данным (1) с
по данным (1) с ![]() ,
, ![]() имеет
вид
имеет
вид![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, 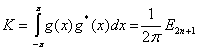 ,
, ![]() ,
, 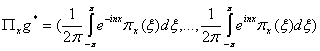 ,
, ![]() - знак
транспонирования,
- знак
транспонирования, ![]() - единичная матрица
размерности
- единичная матрица
размерности ![]() , и оценка
, и оценка ![]() принимает вид
принимает вид
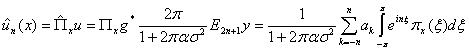 . Введя
обозначение
. Введя
обозначение 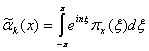 , получаем
оценку
, получаем
оценку ![]() в виде
в виде
![]() ,
, ![]() (4)
(4)
Парето-оптимальная интерполянта
(4) содержит шумовой фон уровня ![]() , который с ростом
, который с ростом ![]() от
от ![]() до
до ![]()
![]() убывает от
убывает от ![]()
![]() до нуля [3]. Ядро парето-оптимальной интерполянты (4) имеет
вид
до нуля [3]. Ядро парето-оптимальной интерполянты (4) имеет
вид
![]() , и его отклонение от ядра
функционала
, и его отклонение от ядра
функционала 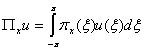 оценивается величиной
операторной невязки [3]
оценивается величиной
операторной невязки [3] ![]()
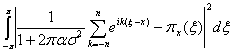 ,
которая с ростом
,
которая с ростом ![]() от
от ![]() до
до ![]() возрастает от
возрастает от ![]() до
до 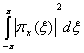 . Операторная невязка косвенно
характеризует величину артефактов парето-оптимальной интерполянты
. Операторная невязка косвенно
характеризует величину артефактов парето-оптимальной интерполянты ![]() . Непосредственной подстановкой
несложно показать, что уровень шумового фона и операторная невязка связаны
соотношением
. Непосредственной подстановкой
несложно показать, что уровень шумового фона и операторная невязка связаны
соотношением ![]() , которое естественно назвать
«законом сохранения». Таким образом, уменьшение величины операторной невязки
приводит к возрастанию величины шумового фона и наоборот. Зависимость
, которое естественно назвать
«законом сохранения». Таким образом, уменьшение величины операторной невязки
приводит к возрастанию величины шумового фона и наоборот. Зависимость ![]() представляет собой множество Парето
рассматриваемой задачи двукритериальной минимизации.
представляет собой множество Парето
рассматриваемой задачи двукритериальной минимизации.
Приведем
примеры парето-оптимальных интерполянт функционала ![]() для конкретных аппаратных функций
для конкретных аппаратных функций ![]() . Пусть
. Пусть ![]() =
=![]() , где
, где
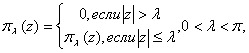
причем 1) ![]() =
=![]() ,
,
2) ![]() ,
,
3) 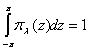 .
.
Тогда 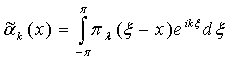 после замены переменных
после замены переменных ![]() принимает вид
принимает вид
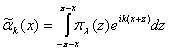
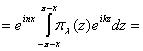
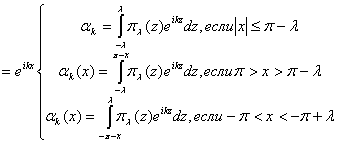
или
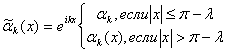 ,
, ![]()
Парето-оптимальная
интерполянта (4) при ![]() имеет вид
имеет вид
![]() ,
, 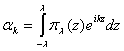 ,
, ![]() . (5)
. (5)
Оценка
(5) при ![]() (в отсутствие шумов)
совпадает с традиционной спектральной оценкой в виде отрезка ряда Фурье с
коэффициентами «спектрального окна» [4]. Следовательно, задача редукции
коэффициентов Фурье к выходу с заданного прибора сводится к суммированию с
весами – «спектральными окнами», причем за счет выбора
(в отсутствие шумов)
совпадает с традиционной спектральной оценкой в виде отрезка ряда Фурье с
коэффициентами «спектрального окна» [4]. Следовательно, задача редукции
коэффициентов Фурье к выходу с заданного прибора сводится к суммированию с
весами – «спектральными окнами», причем за счет выбора ![]() в полученных оценках
шумовой фон можно подавить до нужного уровня.
в полученных оценках
шумовой фон можно подавить до нужного уровня.
Приведем
некоторые конкретные аппаратные функции
и вычислим соответствующие им «спектральные окна».
1) 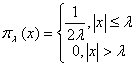
![]() ,
,
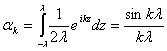 ,
, ![]()
( в этом случае 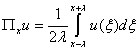 , и мы получаем
оценку усредненного по интервалу
, и мы получаем
оценку усредненного по интервалу ![]() значения
значения ![]() по данным (1)).
по данным (1)).
2)
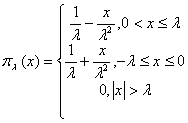 ,
,
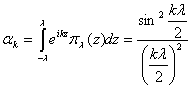 ,
, ![]() ,
,
3) 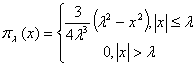 ,
,
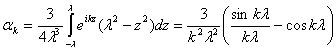 ,
, ![]() ,
,
4) 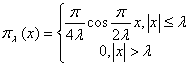 ,
,
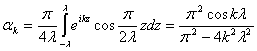 ,
, ![]()
( в случаях 2) – 4) получаем
оценку усредненного по интервалу ![]() значения
значения ![]() с весами
с весами ![]() ).
).
Если
![]() ,
то
,
то ![]() ,
и
,
и ![]() принимают вид
принимают вид
1)![]() , 2)
, 2) 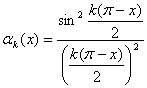 ,
,
3) ![]() ,
4)
,
4) ![]() ,
,
![]() .
.
Замечание. Построенное семейство парето-оптимальных интерполянт (4) зависит от
параметра Парето ![]() . С точки зрения
решения рассматриваемой двукритериальной задачи минимизации операторной невязки
и уровня шумового фона все оценки (4) равнозначны. Однако с изменением величины
. С точки зрения
решения рассматриваемой двукритериальной задачи минимизации операторной невязки
и уровня шумового фона все оценки (4) равнозначны. Однако с изменением величины ![]() один из критериев
возрастает, другой убывает. Поэтому для выбора конкретного значения параметра
парето-оптимизации эксперт (лицо,
принимающее решение) анализирует множество Парето – зависимость
один из критериев
возрастает, другой убывает. Поэтому для выбора конкретного значения параметра
парето-оптимизации эксперт (лицо,
принимающее решение) анализирует множество Парето – зависимость ![]() ,
, ![]() и определяет, что предпочтительней: уменьшить влияние шумовой компоненты, при этом возрастет
искажение артефактами, порожденными неполнотой данных, или наоборот.
и определяет, что предпочтительней: уменьшить влияние шумовой компоненты, при этом возрастет
искажение артефактами, порожденными неполнотой данных, или наоборот.
Для выбора подходящего значения параметра
Парето можно воспользоваться также принципами многокритериальной оптимизации
[3], позволяющими реализовать компромисс между противоречивыми тенденциями
критериев оптимизации.
Таким образом, в данной работе предложен оптимальный метод суммирования рядов Фурье по данным с погрешностями,
основанный на парето-оптимальной редукции данных к выходу с заданного прибора. Указаны приемы подавления
артефактов ![]() -й частичной суммы
ряда, возникающих из-за ограниченности
-й частичной суммы
ряда, возникающих из-за ограниченности ![]() , и уровня шумового фона этой суммы из-за случайных погрешностей
коэффициентов. Одновременно с этим
осуществляется сглаживание частичных сумм за
счет их
усреднения с подходящими весовыми коэффициентами, откуда, как частный случай,
следует суммирование рядов Фурье методом «спектральних окон».
, и уровня шумового фона этой суммы из-за случайных погрешностей
коэффициентов. Одновременно с этим
осуществляется сглаживание частичных сумм за
счет их
усреднения с подходящими весовыми коэффициентами, откуда, как частный случай,
следует суммирование рядов Фурье методом «спектральних окон».
Литература
1. Фихтенгольц Г.М. Основы математического
анализа. Т.1. Изд-е 5-е / Фихтенгольц Г.М. – М.: Наука, 1964. – 440 с.
2. Тихонов А.Н. Методы решения некорректных задач. / Тихонов А.Н., Арсенин
В.Я. – М.: Наука, 1979. – 288 с.
3. Бєлов Ю.А. Математичні методи і алгоритми обробки в задачі інтерпретації
непрямих вимірювань / Бєлов Ю.А., Касьянюк В.С. – К.: Науковий світ, 2000. – 79 с.
4. Хэррис Ф.Дж. Использование окон при гармоническом анализе методом
дискретного преобразование Фурье / Хэррис Ф.Дж. // ТИИЭР, т.66, №1,1978, с.60-96