Сложные системы: Оптимизация и управление

Гарькина И.А., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Как и любая другая научная методология, системный подход опирается на эксперимент и ориентирован на выявление закономерностей, непосредственно следующих из наблюдений и экспериментов, поставленных на основе принятой исследователем теоретической концепции, исходя из целей и задач исследователя (носят прагматический характер). Созданная на основе выявленных факторов и закономерностей модель (модели) объекта фактически заменяет теорию и становится источником последующих выводов и гипотез. Декомпозиция системы субъективна; выбором разбиения системы на подсистемы определяется простота модели системы и возможность ее использования для последующего анализа и прогнозирования ее поведения.

Возможность представления сложной системы конечным множеством моделей, позволяющих исследовать определенное свойство или группу ее свойств по одной или нескольким упрощенным (узкоориентированным) моделям (должны быть проще системы). Создание полной модели для сложной системы практически бесполезно, ибо она будет столь же сложной, как и сама система.

Очевидны преимущества построения математической модели системы на принципах системного анализа с использованием гибкой модульной структуры и с возможностью оптимизации взаимосвязей при максимально возможной унификации модулей по классам систем (для конкретной характеристики объекта используются оригинальные сепаратные модули). Естественно, структурная и параметрическая идентификация с корректировкой характеристик системы при обязательном учете экспериментальных данных, должны осуществляться с требуемой точностью моделирования характеристик. Методика идентификации должна быть увязана с перечнем рассматриваемых характеристик систем (ее структуры и свойств); должен быть разработан перечень допустимых отклонений характеристик модели от характеристик разрабатываемого объекта и методика корректировки характеристик частных моделей (модулей) для устранения указанных отклонений.

Эффективность математического моделирования при синтезе сложных систем в значительной степени определяется тем, насколько точно разработанная иерархическая структура системы отражает взаимодействие между элементами и подсистемами на разных уровнях иерархии. Первичной при проектировании сложной системы является иерархическая структура критериев качества. При необходимости детализация исследуемого объекта производится на ее основе (детализация иерархической структуры критериев качества - задача более простая, чем детализация структуры самой системы).

Многоуровневая иерархическая структура критериев качества сложной системы приводит к необходимости решения задачи многокритериальной оптимизации в условиях неопределенностей целей. Цели часто оказываются противоречащими друг другу. Несмотря на кажущуюся бессмысленность, фраза «добиться максимума производства с минимумом затрат» правильно отражает тенденции, интересы оперирующей стороны. Рассмотренная ситуация типична: она показывает, что, даже зная цели оперирующей стороны, исследователь операции ещё не может приступить к решению оптимизационной задачи. Одновременная оптимизация по всем критериям невозможна в принципе; возможен лишь некоторый компромисс в сочетании требуемых качеств. Например, пусть целевая вектор-функция , – единственный управляемый фактор (рис.1). Решением оптимизационной задачи при ограничении будет ; а при ограничении будем иметь , . Решения же при ограничениях ; вовсе нет, так как интервалы и не перекрываются. Если возможна расстановка приоритетов в критериях качества, задача сводится к однокритериальной оптимизации.

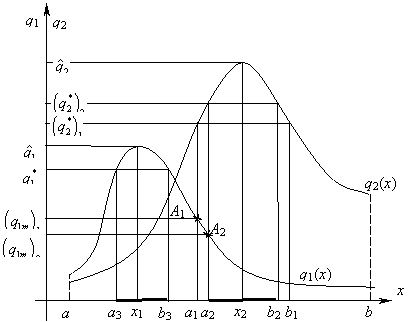
Рис.1. Двухкритериальная задача при одном управляемом факторе

Сталкиваясь с многокритериальными задачами, естественно попытаться найти способы сведения их к задачам с одним критерием, поскольку для однокритериальных задач существуют хорошо разработанные методы решения. Основное их преимущество состоит в простоте интерпретации результатов. Примеры сведения многокритериальной оптимизации к однокритериальной на основе свертывания критериев подробно рассматриваются [1…3].

Литература

1. Гарькина И.А., Данилов А.М., Королев Е.В., Смирнов В.А. Преодоление неопределенностей целей в задачах многокритериальной оптимизации на примере разработки сверхтяжелых бетонов для защиты от радиации / Строительные материалы - Наука. – 2006. -№ 8 . – С.23-26.

2. Данилов А.М., Гарькина И.А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов Строительство. 2011. №1. – С.80-85.

3. Гарькина И.А., Данилов А.М. Управление в сложных технических системах: методологические принципы проектирования / Региональная архитектура и строительство. -№1. 2012. –С.39-42.