Секція „Сучасні методи викладання ”

Житарюк І.В.

Чернівецький національний університет імені Юрія Федьковича, Україна

МІЖПРЕДМЕТНІ ЗВ’ЯЗКИ АЛГЕБРИ І ТРИГОНОМЕТРІЇ

Міжпредметність – сучасний принцип навчання, який впливає на відбір і структуру навчального матеріалу низки предметів, посилюючи системність знань його суб’єктів, активізує методи навчання, орієнтує на застосування комплексних форм організації останнього.

Відомо, що певний матеріал із загальноосвітнього курсу математики засвоюється суб’єктами навчання не тоді, коли він є метою навчання, а коли цей матеріал стає засобом для розв’язування інших завдань [1]. Тому доцільно показати учням як можна застосовувати деякі властивості тригонометричних функцій і співвідношень між ними при розв’язуванні, наприклад, алгебраїчних задач. При цьому переслідуються цілі: провести міжпредметні зв’язки між тригонометрією і алгеброю, сприяти формуванню в суб’єктів навчання умінь розв’язувати деякі види рівнянь алгебри за допомогою тригонометричних підстановок.

Проілюструємо сказане на прикладі розв’язання рівняння

.

Спробувавши виконати піднесення до квадрату обох частин рівняння, суб’єкти навчання отримають рівняння 6-го степеня, розв’язування яких у загальноосвітному курсі математики не передбачено. Звернувши увагу учнів, на те, що областю допустимих значень змінної даного рівняння є відрізок [- 1; 1], учитель пропонує згадати вивчені функції, областю значень яких є цей відрізок. Після чого робиться висновок: якщо з умови завдання випливає, що допустимі значення змінної x визначаються нерівністю |x|≤1, то можна зробити заміни х=sinα, або х=cosα , причому яку з них вибрати, залежить від конкретного завдання.

Оскільки права частина заданого рівняння, тобто 4х³-3х, існує при довільних значеннях х, а ліва – при хÎ[-1; 1], то введемо заміну х=cosα. Виберемо для зручності довільний відрізок, на якому косинус набуває значення від -1 до 1, наприклад, відрізок [0; p].

Підставимо х=cosα у рівняння, отримаємо

.

Звідси із урахуванням того, що

sin²α+cos²α=1 i 4cos³α-3cosα=cos3α

матимемо

|sinα|=cos3α.

Оскільки αÎ[0; p], то sinα≥0, тому модуль можна опустити:

sinα= cos3α,

sinα-cos3α=0.

Врахувавши, що sinx=cos(p/2-α), отримаємо

cos(p/2-α)-cos3α=0.

Скориставшись формулою

cosα-cosβ=2sinsin,

одержимо

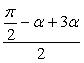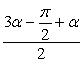2sinsin=0

або

sinsin=0.

Звідки

sin=0 або sin=0.

Розв’язками отриманих рівнянь є

,

.

Звідси

,

.

Умові αÎ[0; p] з отриманих значень α задовольняють лише три

.

Врахувавши заміну х=cosα, отримуємо

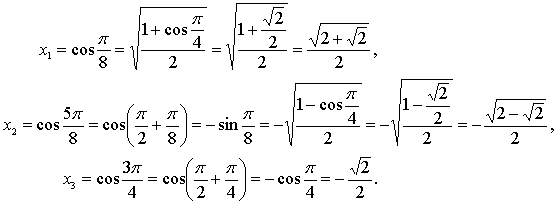
Таким чином, розв’язками заданого рівняння є , - .

Література

1. Калинин С.И. Задачи и упражнения по началам математического анализа [Текст] / Калинин С.И., Канин Е.С., Маянская Г.М., Ончукова Л.В., Подгорная И.И., Фалелеева С.А. – Киров : ВГПУ, 1997. – 208 с.

2. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе [Текст] / Мордкович А.Г. // Математика в школе. – 2002. – № 6 – С. 32-38.

3. Панчишкин А.А. Тригонометрические функции в задачах [Текст] / Панчишкин А.А., Шавгулидзе Е.Т. – Москва : Наука, 1986. – 160 с.