Биологические науки /11. Биоинженерия и биоинформатика

Ганенко А.С., к.ф.-м.н. Баландин В.А., к.т.н. Аждер Т.Б.

Московский технологический университет, Россия

Вейвлет-анализ в работе с электрокардиограммами

Современная медицинская диагностика – сложный процесс получения достоверных и точных знаний о состоянии и функционировании и организма в целом и отдельных его систем. В этой связи одной из проблем является улучшение и повышение качества результатов исследований. Электрокардиография в настоящее время является ведущим методом диагностики сердечной деятельности. Это связано с тем, что электрокардиограмма является основным показателем, позволяющим вести профилактический и лечебный контроль сердечнососудистых заболеваний.

Классический подход в электрокардиологии состоит в использовании различных методик анализа временных зависимостей амплитуды кардиосигнала: стандартное ЭКГ-измерение, измерение частоты сердечных сокращений, дисперсия реполяризации и т. д. Однако существующие стандартные методы анализа временной области не всегда достаточны для описания всех особенностей ЭКГ-сигнала и не позволяют в полной мере выявить его характерные черты

В этой связи новые возможности открывает использование в электрокардио-логии вейвлет-преобразования для получения частотно-временного представления сигнала. Вейвлет-преобразование основано на использовании набора анализирующих функций (вейвлетов) для разложения по ним ЭКГ-сигнала на последовательность коэффициентов. Каждый вейвлет имеет определенную длительность, положение во времени и полосу частот. В результате преобразования вейвлет-коэффициенты отражают ЭКГ-компоненты на некотором временном отрезке и соответствующей полосе частот.

Выбор того или иного класса анализирующих функций вейвлет-преобразования диктуется так же спецификой задачи, а именно тем, какую информацию нужно извлечь из сигнала. В ряде случаев с помощью различных вейвлетов можно более полно выявить особенности анализируемого сигнала.

В нашей работе мы выполнили детальное исследование кардиосигнала для выделения в нем PQRST-признаков с помощью вейвлет-инструментария математического пакета MATLAB. Задачей был выбор оптимального вейвлета, способного выделять интересующие участки экг. Под оптимальным вейвлетом понимается тот, который обеспечивает лучшую идентификацию местоположения девяти точек кардиоцикла: начало, пик и окончание (смещение) P-зубца, QRS-комплекса и T-зубца. Для этого было протестировано несколько вейвлет-функций: вейвлет-функция Гаусса, Морле, а также биортогональный вейвлет. Исследование проводилось для двух полных комплексов PQRST ЭКГ сигнала одного пациента. Сигнал был взят из международного научного ресурса «Physionet».

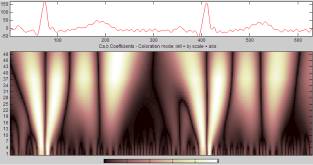
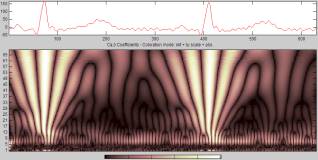
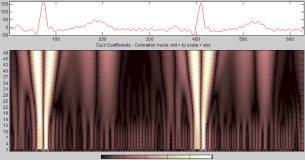
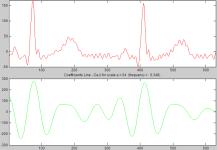
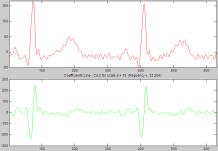
Ниже представлены спектрограммы (Рисунок 1, 2, 3), полученные при помощи непрерывного вейвлет-преобразования одного и того же кардиосигнала с использованием трех указанных выше вейвлетов. По вертикальной оси на спектрограмме отображены значения масштабного параметра, а по горизонтальной – время, представленное в условных отсчетах (продолжительность каждого комплекса составляет 0.7 секунд).

Рисунок 1. Вейвлет Гаусса.	Рисунок 2. Вейвлет Морле.
Рисунок 3. Биортогональный вейвлет 1.5.

Вейвлет-преобразование анализируемого сигнала осуществлялось следующим образом: для выбранного значения масштабного параметра a производилась операция свертки сигнала ЭКГ с вейвлетом для всего диапазона значений сдвига. Таким образом, вейвлет с заданным значением a как бы «пробегает» по всему исследуемому сигналу, в результате на выходе получается массив вейвлет-коэффициентов (С), размер которого соответствует количеству отсчетов исходного сигнала, а величина определяется выражением:

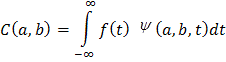
где С – вейвлет-коэффициент, a – масштабный параметр, b – момент времени, - вейвлет-функция, f(t) – сигнал. Далее выбирается следующий масштабный коэффициент и процедура повторяется.

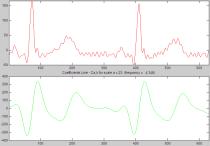
Рисунок 4. Процесс перемещения вейвлета вдоль исследуемого сигнала.

Нам нужно было определить значения масштабного параметра, при которых видны девять точек кардиоцикла и оценить погрешность их нахождения. Все результаты, представленны в таблицах 1, 2, 3.

Таблица 1 - Вейвлет Гаусса.

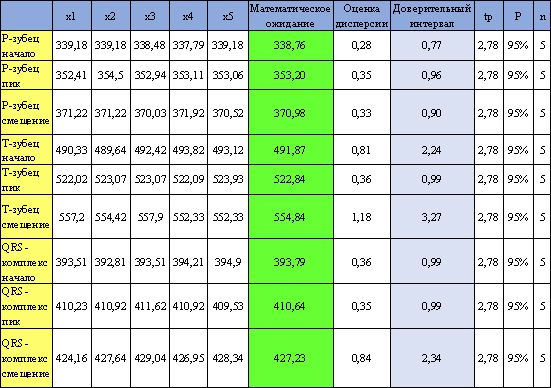
Таблица 2 - Вейвлет Морле.

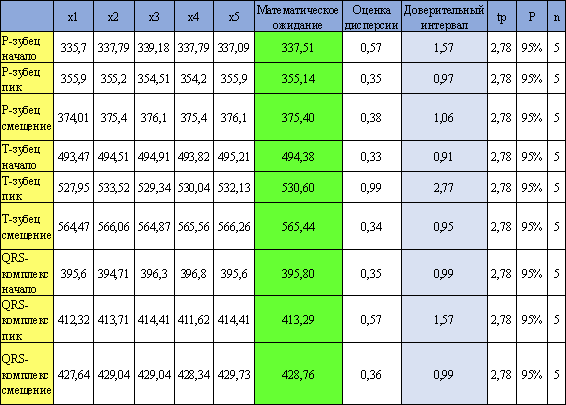
Таблица 3 – Биортогональный вейвлет.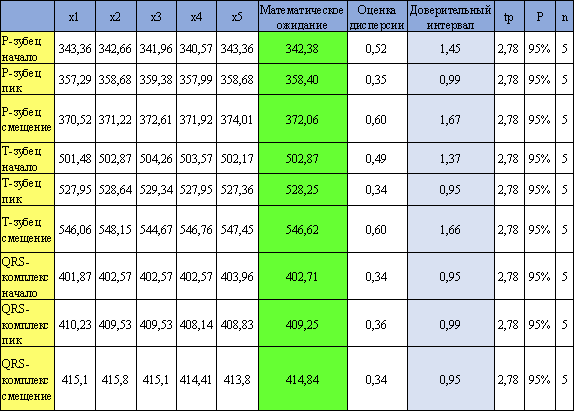

Здесь x1..x5 – условные отсчеты начала/пика/смещения, tp – критерий Стьюдента, P – вероятность, а n – количество измерений.

Из полученных результатов следует, что вейвлет Гаусса (Рисунок 4) наилучшим образом подходит для изучения P-зубца, вейвлет Морле (Рисунок 5) лучше других описывает T-зубец, а для QRS-комплекса в большей степени подходит биортогональный вейвлет (Рисунок 6). Подводя итог, можно отметить, что каждый из трех исследованных вейвлетов может использоваться при исследованиях кардио-сигнала, но с разной эффективностью для различных его участков.

Рисунок 5. Вейвлет Гаусса, масштаб 23.

Рисунок 6. Вейвлет Морле, масштаб 64.

Рисунок 7. Биортог-ональный вейвлет, мас-штаб 15.

Литература:

1. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в MATLAB/Смоленцев Н.К.-М.:ДМК Пресс, 2008.-448с.

2. Misiti M., Misiti Y.: Wavelet ToolboxTM 4 User’s Guide ⓒ COPYRIGHT 1997–2009 by The MathWorks, Inc. -153с.

3. Ресурс для медико-биологических исследований и разработок https://physionet.org