Современные информационные технологии / 3. Программное обеспечение

Чернявский М.А.

Харьковский национальный университет радиоэлектроники

ИСПОЛЬЗОВАНИЕ МЕТОДА МОНТЕ-КАРЛО ДЛЯ ПЛАНИРОВАНИЯ И ИДЕНТИФИКАЦИИ РИСКОВ

В IT-ПРОЕКТЕ

Метод Монте-Карло является группой численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи [1]. Данный метод применяют для идентификации прогнозных значений рисков, результатов низкоформализованных и стохастических активностей, когда экспертные и аналитические методы затруднительно применить из-за сложности и комплексности рисковой области.

Входными данными для моделирования методом Монте-Карло являются хорошо проработанная модель системы, информация о типе входных данных, источниках неопределенности и требуемых выходных данных. Входные данные и соответствующую им неопределенность рассматривают в виде случайных переменных с соответствующими распределениями. Часто для этих целей используют равномерные, треугольные, нормальные и логарифмически нормальные распределения.

Результатом анализа выступает распределение вероятностей возможных результатов проекта. Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров  получить распределение доходности проекта [2].

Процесс идентификации включает следующие этапы:

· Определение модели или алгоритма, которые наиболее точно описывают поведение исследуемой системы. Модель записывают в форме уравнения, выражающего соотношение между входными и выходными параметрами.

· Многократное применение модели для получения выходных данных модели (моделирование системы). Значения, отобранные в качестве входных данных, получают исходя из соответствующих распределений вероятностей, характеризующих неопределенности данных.

· С помощью СППР многократно используют модель с различными входными данными и получают выходные данные. Они могут быть обработаны с помощью статистических методов для получения оценок среднего, стандартного отклонения, доверительных интервалов.

Неопределенность, которую требуется усреднить, составляют оценки отобранных заранее экспертов.

Модель представлена следующей формулой:

, где

– оценка вероятности возникновения риска n;

- оценка степени опасности риска n;

– весовой коэффициент компетентности эксперта m;

- вес риска n;

– итоговая оценка риска n экспертом m.

Формула составлена таким образом, что к дальнейшему рассмотрению будут приниматься риски, итоговая оценка которых будет выше нуля (с учетом погрешности).

Для каждого отдельного риска составляется таблица вероятностей, основанная на оценках экспертов (таблица 1).

Таблица 1 – Таблица вероятностей риска n с весом .

	Вероятность возникновения	Степень опасности		Итоговая оценка
Порядковый номер эксперта(m)	Оценка	Оценка
1
2
…
m

Далее по значениям итоговой оценки риска, программное средство рассчитает предел погрешности, исходя из среднего значения и среднеквадратического отклонения.

Было принято решение принять 95% за доверительный интервал, чтобы исключить слишком большую разницу в значениях, но сохранить большинство оценок.

Формула среднего значения выборки:

= , где

- сумма значений ряда;

- количество значений ряда.

Формула среднеквадратического отклонения:

, где

– среднее значение квадратов разности от среднего (дисперсия).

Формула предела погрешности:

, где

- коэффициент доверия, табличная величина, определяемая - доверительным интервалом.

Исходя из этих данных, можно будет определить, будут ли рассматриваться методы по предотвращению либо ликвидации данного конкретного риска.

Да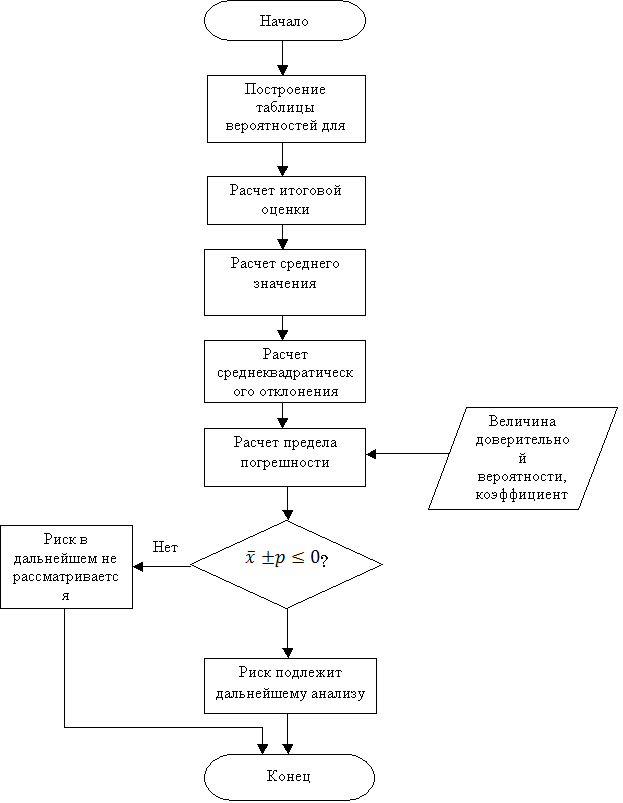

Схема алгоритма обработки данных приведена на рисунке 1

Рисунок 1 – Схема алгоритма

Литература:

1. Статья «Моделируя жизнь», автор Андрей Тепляков. Журнал «Hard’n’Soft» №7 2001г.

2. Национальный стандарт РФ ГОСТ Р ИСО/МЭК 31010-2011 "Менеджмент риска. Методы оценки риска".