А. Кадиримбетова
Таразский государственный университет им. М.Х.Дулати,
Казахстан
НЕЛИНЕЙНОЕ
ГРАНИЧНОЕ УПРАВЛЕНИЕ ТЕПЛОВЫМ ПРОЦЕССОМ, ОПИСЫВАЕМЫМ
ФРЕДГОЛЬМОВО ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ
.
Исследована
задачи нелинейного граничного управления тепловым процессом, описываемым
фредгольмово интегро-дифференциальным уравнением. Указан алгоритм построения
приближенного решения задачи оптимизации и доказан его сходимость.
Ключевые слова: Функционал, краевая
задача, граничное управление, оптимальное управление, нелинейное интегральное
уравнение, приближенное решение, сходимость.
I. Постановка задачи оптимизации и нелинейное
интегральное уравнение оптимального управления
В статьях [1-2] рассмотрена задача
нелинейной оптимизации, где требуется минимизировать квадратичный функционал
![]()
![]() (1)
(1)
на множестве решений краевой задачи
![]()
![]()
![]() (2)
(2)
![]()
![]() (3)
(3)
![]()
![]()
![]() (4)
(4)
Здесь функция ![]()
![]()
![]() -описывает состояния управляемого
процесса, ядро
-описывает состояния управляемого
процесса, ядро ![]() –известная
функция, определенная в квадрате
–известная
функция, определенная в квадрате ![]()
![]() и удовлетворяющая условию
и удовлетворяющая условию
![]() (5)
(5)
![]()
![]()
![]()
![]() -заданные функции, причем функция
-заданные функции, причем функция![]() нелинейно зависит от функции управления
нелинейно зависит от функции управления ![]() и по функциональной переменной
и по функциональной переменной ![]() монотонна, т.е.
монотонна, т.е.
![]() (6)
(6)
![]() параметр, постоянная
параметр, постоянная ![]() ,
,![]() -фиксированный
момент времени,
-фиксированный
момент времени,![]() -гильбертово
пространство функций, определенных на множестве
-гильбертово
пространство функций, определенных на множестве ![]() .
.
Решение краевой задачи определяется по
формуле
![]()
где ![]() -решение
линейного интегрального уравнения
-решение
линейного интегрального уравнения
![]() ,(7)
,(7)
с ядром
![]() (8)
(8)
и свободным членом
![]() (9)
(9)
Коэффициенты Фурье ![]() находим
по формуле [3]
находим
по формуле [3]
![]()
где резольвента ![]() ядра
ядра ![]() имеет
вид
имеет
вид
![]()
![]()
![]() (11)
(11)
и при выполнении условия
![]() , (12)
, (12)
является непрерывной функцией, а также
удовлетворяет оценке
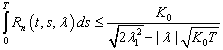 ,
,![]() . (13)
. (13)
Установлено, что оптимальное управление ![]() определяется как решение нелинейного
интегрального уравнения
определяется как решение нелинейного
интегрального уравнения
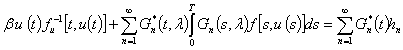 , (14)
, (14)
где
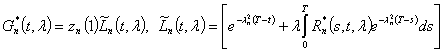 (15)
(15)
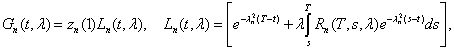 (16)
(16)
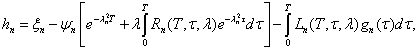 (17)
(17)
удовлетворяющее дополнительному условию
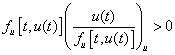 .(18)
.(18)
Условие (18)ограничивает класс функций
граничных воздействий ![]() .
Поэтому будем считать, что функция
.
Поэтому будем считать, что функция ![]() удовлетворяет условию (18) для любого управления
удовлетворяет условию (18) для любого управления ![]() .
Доказано [2], что интегральное уравнение (14)
в пространстве
.
Доказано [2], что интегральное уравнение (14)
в пространстве ![]() имеет
единственное решение
имеет
единственное решение
![]() (19)
(19)
где ![]() определяется
единственным образом как предел приближенных решений
определяется
единственным образом как предел приближенных решений ![]() нелинейного интегрального уравнения
нелинейного интегрального уравнения
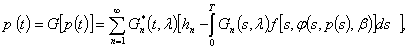 (20)
(20)
и удовлетворяет оценке
![]()
для любого произвольного элемента ![]() .
.
Оптимальный процесс ![]() определяется по формуле
определяется по формуле
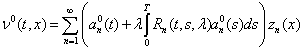 ,
,
где
![]() . (21)
. (21)
Минимальное значение функционала (1) вычисляется по формуле
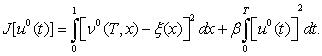 (22)
(22)
Тройка ![]() определяет решения задачи нелинейной
оптимизации. Нетрудно заметить, что построить точное решение задачи оптимизации
не всегда удается. Поэтому на практике ограничиваются нахождением
определяет решения задачи нелинейной
оптимизации. Нетрудно заметить, что построить точное решение задачи оптимизации
не всегда удается. Поэтому на практике ограничиваются нахождением![]() -го
приближения
-го
приближения![]() точного
решения и доказывает сходимость приближений точному решению
точного
решения и доказывает сходимость приближений точному решению ![]() .
.
II Приближенное решение задачи оптимизации
и его сходимость.
1.
Приближения оптимального управления и их сходимость.
k-е
приближение оптимального управления находим по формуле
![]() (23)
(23)
Лемма 2.1. Пусть функция ![]() удовлетворяет условию Липщица по
функциональной переменной
удовлетворяет условию Липщица по
функциональной переменной ![]() ,
т.е.
,
т.е.
![]()
![]() (24)
(24)
Тогда ![]() -е
приближение сходится к оптимальному управлению
-е
приближение сходится к оптимальному управлению ![]() по норме гильбертово пространства
по норме гильбертово пространства ![]() .
.
Доказательство. Утверждение леммы следуетиз
неравенства
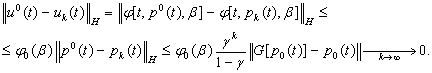 (25)
(25)
2.
Приближения оптимального процесса и их сходимость.
При построении приближений оптимального
процесса ![]() будем различать следующие приближения:
будем различать следующие приближения:
2.1.m-е приближение оптимального процесса по резольвенту находим по формуле
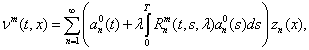
где
![]()
m-ое приближение резольвенты ![]() ;
;
2.2. m, k-е приближение оптимального процесса находим по
формуле
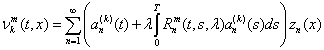 ,
,
где
![]() .
.
2.3.
m, k, r-ое приближение оптимального процесса находим по
формуле
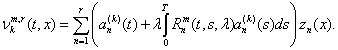
Лемма 2.2. m-е приближение![]() сходится к оптимальному процессу
сходится к оптимальному процессу ![]() по норме пространства H(Q).
по норме пространства H(Q).
Доказательство следует из соотношения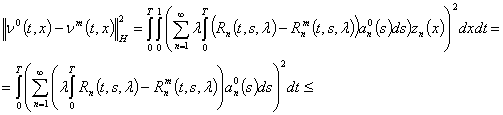
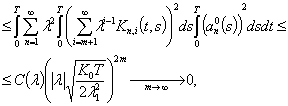
где ![]() -
ограниченнаяположительнаяпостоянная. Это соотношение устанавливается
непосредственно вычислением и имеет
место, т.к.
-
ограниченнаяположительнаяпостоянная. Это соотношение устанавливается
непосредственно вычислением и имеет
место, т.к.
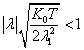 .
.
Лемма 2.3. Пусть функция ![]() удовлетворяет условию Липщица по функциональной переменной
удовлетворяет условию Липщица по функциональной переменной ![]() ,
т.е.
,
т.е.
![]() .(26)
.(26)
Тогда ![]() -е
приближениепри
-е
приближениепри ![]() сходится к
сходится к![]() по норме гильбертово
пространства
по норме гильбертово
пространства ![]() для любого
для любого ![]()
Доказательство. Непосредственными
вычислениями имеем соотношение
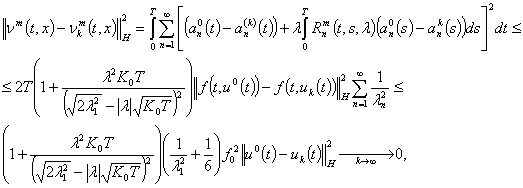
при любом
фиксированном ![]() , из которого следует утверждение леммы.
, из которого следует утверждение леммы.
Лемма 2.4. k,m,r-е приближение при ![]() сходится к функции
сходится к функции ![]() по норме пространства
по норме пространства ![]() для любого k,m = 1,2,3,… .
для любого k,m = 1,2,3,… .
Доказательство.
Непосредственным вычислением имеем
соотношение
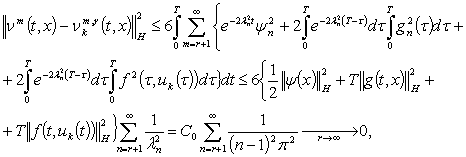
как остаточный член сходящегося ряда, из которого следует утверждение леммы.
Теорема
2.1. k,m,r-е приближение при![]() сходится к оптимальному процессу
сходится к оптимальному процессу ![]() по норме пространства
по норме пространства ![]() .
.
Доказательство.
Согласно лемм 2.2. – 2.4. утверждение
теоремы следует из соотношения
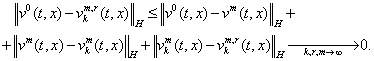
III.Приближения минимального значения
функционала и ихсходимость.
В
соответствие с приближениями ![]() оптимального процесса
оптимального процесса ![]() будем различать следующие виды приближений
минимального значения функционала
будем различать следующие виды приближений
минимального значения функционала ![]()
3.1.m-е
приближение по резольвенту минимального значения функционала находим по формуле
![]()
3.2. m, k-е приближение минимального значения функционала находим по формуле
![]()
3.3.
m, k, r-ое приближение минимального значения функционала находим по формуле
![]()
Леммы
3.1. Приближение ![]() при
при![]() сходится к значению функционала
сходится к значению функционала ![]() .
.
Доказательство.Непосредственным вычислением имеем соотношение
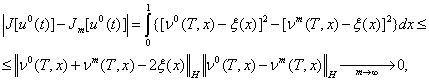
из которого следует утверждение леммы.
Леммы
3.2. Приближение ![]() при
при![]() сходится к значению функционала
сходится к значению функционала ![]() для любого m =1,2,3,….
для любого m =1,2,3,….
Доказательство.
Непосредственным вычислением имеем
соотношение
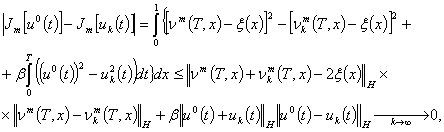
из которого следует утверждение леммы.
Леммы
3.3. Приближение ![]() при
при![]() сходится к значению функционала
сходится к значению функционала ![]() для любых k,m =1,2,3,….
для любых k,m =1,2,3,….
Доказательство.
Непосредственным вычислением имеем
соотношение
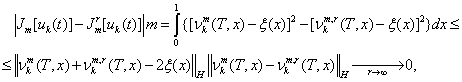
из которого следует утверждение леммы.
Теорема
3.1. Приближение ![]() при
при![]() сходится к значению функционала
сходится к значению функционала ![]() .
.
Доказательство.
Согласно лемм 3.1.-3.3 утверждение
теоремы следует из соотношения
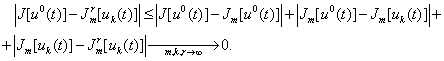
Литература
1.
Керимбеков А.,
Кадиримбетова А.К. О разрешимости задачи нелинейного граничного управления
тепловым процессом, описываемым фредгольмово интегро-дифференциальным
уравнением. //
Вестник ОшГУ,спец.вып.–Ош: 2013, №1. – С. 167-172.
2.
Керимбеков А.,
Кадиримбетова А.К. Решение одной задачи теории нелинейных интегральных
уравнений. //
Вестник ОшГУ, спец.вып. –Ош: 2013, №1. – С. 176-173.
3.
Краснов М.В.
Интегральные уравнения. - М.: Наука, 1975.-303с.