Р.Ж.Наметкулова

Таразский государственный университет им.М.Х.Дулати, Казахстан

ОБ ОДНОЙ ЗАДАЧЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕПЛОВЫМИ ПРОЦЕССАМИ

Исследованы вопросы однозначной разрешимости нелинейного интегрального уравнения специфического вида и указан алгоритм построения его решения. Установлены достаточные условия существования единственного решения.

Ключевые слова: Нелинейное интегральное уравнение, оптимальное управление, принцип сжимающих отображений, метод последовательных приближений.

При изучении задачи оптимального управления процессами, описываемыми уравнениями в частных производных, в случаях, когда функция внешнего источника нелинейно зависит от функции управления, искомое оптимальное управление определяется как решение нелинейного интегрального уравнения и удовлетворяет дополнительному условию в виде неравенства [1,2]. Такие задачи недостаточно изучены в теории интегральных уравнений, т.е. не разработана методика решения интегральных уравнений, содержащих неизвестную функцию, как под интегралом, так и вне интеграла. В данной работе рассматриваются вопросы однозначной разрешимости одной из таких задачи.

Рассмотрим нелинейное интегральное уравнение вида

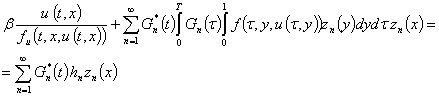(1)

с дополнительным условием

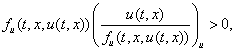(2)

где неизвестная функция, заданная функция,

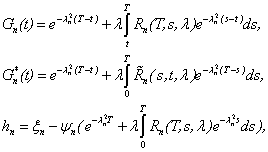
известные функции, удовлетворяющие следующим оценкам

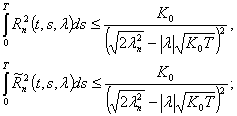₍₃₎

ортонормированная(в гильбертовом пространстве ) система собственных функций краевой задачи

а соответствующие им собственные значения, которые удовлетворяют следующим неравенствам

(4)

- параметр, постоянная- фиксированный момент времени.

Вопрос однозначной разрешимости нелинейного интегрального уравнения (1) исследуем согласно методике разработанной проф. Керимбековым А. [3].

Положим

.

Согласно условию (2) это равенство разрешается относительно функции , т.е. существует функция , такая что

(5)

Уравнение (1) перепишем в виде

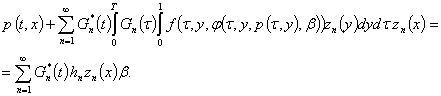₍₆₎

Введя обозначения

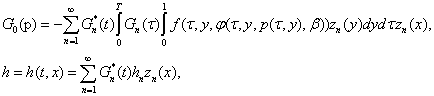(7)

уравнение (6) перепишем в операторной форме

(8)

Лемма-1: Функция является элементом гильбертово пространства , т.е..

Доказательство. Утверждение леммы следует из неравенства

где

Лемма-2:Функция является элементом гильбертово пространства , т.е.

Доказательство.Утверждение леммы следует из неравенства

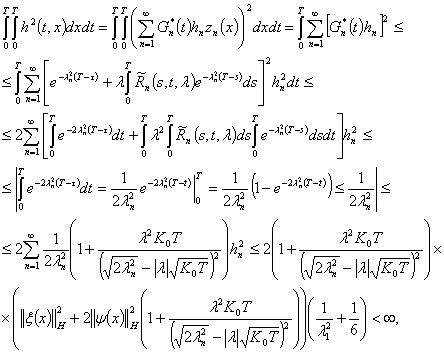
которое устанавливается непосредственно вычислением.

Лемма-3: Оператор переводит пространство в себя.

Доказательство. Непосредственным вычислением имеем соотношение

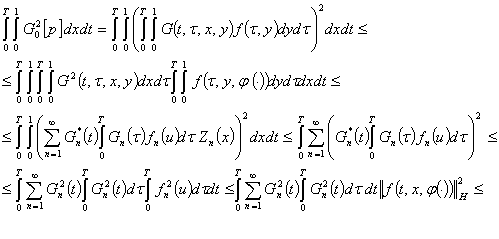
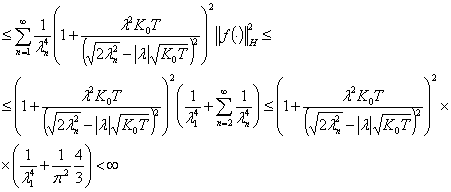
из которого следует утвеждение леммы.

Лемма-4: Пусть функция удовлетворяет условию Липшица по функциональной переменной ,а функция по функциональной переменной . Тогда при выполнении условия

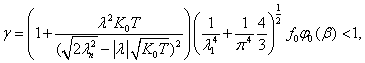
где - положительные постоянные, оператор является сжимающим.

Доказательство.Утверждение леммы следует из соотношения

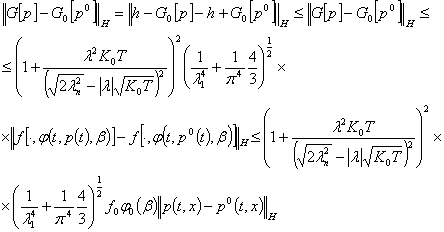
Теорема. При выполнении условий Лемм 1-4 операторное уравнение (8) имеет единственное решение в пространстве .

Доказательство. При выполнении условий лемм 1-4 имеет место принцип сжимающих отображений[4].

Решение операторного уравнения (8) строится методом последовательных приближений по следующей схеме

и удовлетворяет оценке

где - точное решение операторного уравнения (8).

Оптимальное управление находим по формуле

Функция является единственным решением нелинейного интегрального уравнения (1). Это решение, быть может, не всегда удовлетворяет условию (2). Поэтому берется из класса функций удовлетворяющих условию (2).

Литература

1. КеримбековА., Наметкулова Р.Ж.Решение задачи нелинейной оптимизации теплового процесса, описываемым фредгольмово интегро-дифференциальным уравнением. // Вестник КРСУ, –2014, Т.14, №1. – С. 166-172.

2. Наметкулова Р.Ж.Приближенное решение задачи нелинейной оптимизации теплового процесса, описываемого фредгольмово интегро-дифференциальным уравнением. // Вестник КРСУ, –2013, Т.13, №7. – С. 23-27.

3. Керимбеков А.К. Нелинейное оптимальное управление линейными системами с распределенными параметрами. –Дисс… докт. физ.-мат наук. Институт математики НАН КР. – Бишкек, 2003. – 224с.

4. Люстерник Л.А., Соболев В.И. Элементы функционального анализа.- М.: Наука, 1965.-520 с.