Педагогические науки / 5.Современные методы преподавания.
Ауельбекова Нурипа Кененбаевна
Алматы қаласы Алатау ауданы №26 жалпы білім
беретін мектебі
ПАРАБОЛА
БОЙЫНДАҒЫ ![]() ТҮЗУІНЕ ДЕЙІНГІ АРАЛЫҒЫ ЕҢ
ҚЫСҚА НҮКТЕНІ ТАБУ
ТҮЗУІНЕ ДЕЙІНГІ АРАЛЫҒЫ ЕҢ
ҚЫСҚА НҮКТЕНІ ТАБУ
Қысқаша мазмұны:кез келген бір түзуге
дейінгі аралығы ең қысқа болатын, параболаның
бойындағы бір нүктені табу тәсілі мектеп математика
оқулығында айтылмаған болса да, бағдарламалық
білімдерді пайдаланып, шындыққа жанасатын ой пікірлерді
ортаға қоямын.
Егер парабола мен ![]() (
(![]() сандары бір уақытта
нөлге тең болмайды) түзуі қилыспайтын
болса, онда
сандары бір уақытта
нөлге тең болмайды) түзуі қилыспайтын
болса, онда![]() түзуіне дейінгі аралығы ең
қысқа болатын, параболаның бойындағы бір нүктені
төмендегі теоремалар бойынша өте оңай табуымызға болады.
түзуіне дейінгі аралығы ең
қысқа болатын, параболаның бойындағы бір нүктені
төмендегі теоремалар бойынша өте оңай табуымызға болады.
1 – теорема: ![]() (
(![]() ) түзуіне дейінгі аралығы ең
қысқа болатын,
) түзуіне дейінгі аралығы ең
қысқа болатын, ![]() ; (
; (![]() ) параболасының бойындағы бір
нүктені
) параболасының бойындағы бір
нүктені ![]() деп, ал ең қысқа аралықты
деп, ал ең қысқа аралықты![]() десек, онда мынадай болады.
десек, онда мынадай болады.
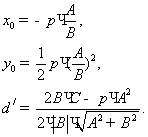
( мұндағы ![]() ,
,![]() )
)
1 – ші дәлелдеу тәсілі: бұл қорытындыны
туындыны қолданып дәлелдесек өте оңай болады.
![]() параболасын
параболасын ![]() түрінде жазып алып, осы параболаның
түрінде жазып алып, осы параболаның ![]() түзуіне параллель болатын
түзуіне параллель болатын ![]() нүктесіндегі жанамасының
бұрыштық кооэффициентін қарастырайық. Яғни
нүктесіндегі жанамасының
бұрыштық кооэффициентін қарастырайық. Яғни
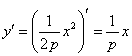 болып,
болып, ![]() болады. Ал
болады. Ал ![]() теңдеуін, түзу
теңдеуінің бұрыштық кооэффициентімен берілген
түріне келтірсек
теңдеуін, түзу
теңдеуінің бұрыштық кооэффициентімен берілген
түріне келтірсек ![]() болып,
болып, ![]() шығады. Сондықтан
шығады. Сондықтан ![]() болып,
болып, ![]() болады.
болады. ![]() дің бұл мәнін
дің бұл мәнін ![]() теңдеуіндегі орынына қойсақ
теңдеуіндегі орынына қойсақ ![]() шығады. Сонымен
шығады. Сонымен 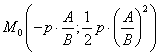 болады. Енді ең қысқа
аралықты табайық. Нүктеден түзуге дейінгі
арақашықтықты табу формуласы бойынша
болады. Енді ең қысқа
аралықты табайық. Нүктеден түзуге дейінгі
арақашықтықты табу формуласы бойынша 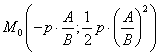 нүктесінен
нүктесінен ![]() түзуіне дейінгі
қашықтықты табамыз.
түзуіне дейінгі
қашықтықты табамыз.
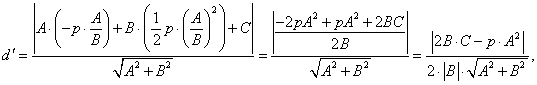
![]() болғандықтан,
болғандықтан, 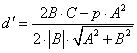 шығады. Сондықтан теорема
оңай дәлелденеді. Яғни
шығады. Сондықтан теорема
оңай дәлелденеді. Яғни
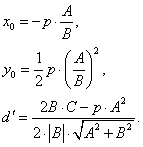
( мұндағы ![]() болады.)
болады.)
Төменде осы теореманы алгебралық
әдіспен дәлелдейік. (Туындыны үйренбеген 8 – 9 – шы сынып
оқушылары үшін өте қажетті.)
2 – ші дәлелдеу:![]() нүктесі
нүктесі ![]() ; (
; (![]() ),
),
параболасының бойындағы бір нүкте
болғандықтан, ![]() теңдігі орындалып
теңдігі орындалып ![]() болады.
болады.
Сондықтан![]() болады да, нүктеден түзуге дейінгі ара
қашықтықты табу формуласынан мынау шығады.
болады да, нүктеден түзуге дейінгі ара
қашықтықты табу формуласынан мынау шығады.
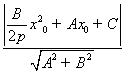
![]()
![]() нүктесінен
нүктесінен![]() (
(![]() ) түзуіне дейінгі аралық ең
қысқа болады деген шартқа сүйенсек, онда өрнек
) түзуіне дейінгі аралық ең
қысқа болады деген шартқа сүйенсек, онда өрнек ![]() — дің ең кіші мәнін табуымыз
қажет болады.
— дің ең кіші мәнін табуымыз
қажет болады.
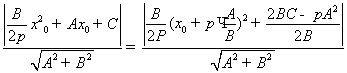
![]() болатындықтан,
болатындықтан, ![]() тұрақты сан екенін ескерсек,
тұрақты сан екенін ескерсек, 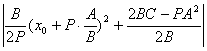 өрнегі ең кіші мән
қабылдауы керек. Оны мына екі түрлі жағдайға
бөліп талқылауға болады.
өрнегі ең кіші мән
қабылдауы керек. Оны мына екі түрлі жағдайға
бөліп талқылауға болады.
![]()
![]() болса,
болса, ![]() болғандықтан,
болғандықтан,
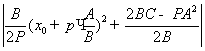 өрнегі ең кіші мән
қабылдауы үшін
өрнегі ең кіші мән
қабылдауы үшін ![]() болу шарты бойынша
болу шарты бойынша ![]() болуы тиіс.
болуы тиіс.
Бұдан ![]() болып,
болып, ![]() шығады.
шығады.
![]()
![]() болса,
болса, ![]() болғандықтан,
болғандықтан,
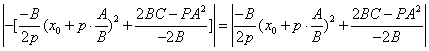 болып, ең кіші мән
қабылдауы үшін
болып, ең кіші мән
қабылдауы үшін![]() болу шарты бойынша
болу шарты бойынша ![]() болуы керек. Бұдан
болуы керек. Бұдан ![]()
![]()
![]() шығады.
шығады.
![]() - пен
- пен ![]() -тан
-тан ![]() ; (
; (![]() ) болады.
) болады. ![]() - дің бұл мәнін
- дің бұл мәнін ![]() өрнегіндегі орынына қойсақ,
өрнегіндегі орынына қойсақ, ![]() болады. Ал,
болады. Ал, 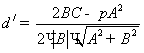 шығады. ( Бұлардағы
шығады. ( Бұлардағы ![]() ,
,![]() )
)
2 – теорема:![]() (
(![]() ) түзуіне дейінгі аралығы ең
қысқа болатын,
) түзуіне дейінгі аралығы ең
қысқа болатын, ![]() ; (
; (![]() ) параболасының бойындағы бір
нүктені
) параболасының бойындағы бір
нүктені ![]() деп, ал ең қысқа аралықты
деп, ал ең қысқа аралықты![]() десек, онда мынадай болады.
десек, онда мынадай болады.
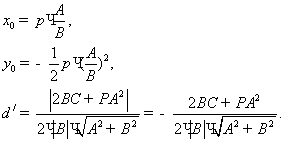
(мұндағы ![]()
![]() )
)
3 – теорема:![]() (
(![]() ) түзуіне дейінгі аралығы ең
қысқа болатын,
) түзуіне дейінгі аралығы ең
қысқа болатын, ![]() ; (
; (![]() ) параболасының бойындағы бір
нүктені
) параболасының бойындағы бір
нүктені ![]() деп, ал ең қысқа
аралықты
деп, ал ең қысқа
аралықты![]() десек, онда мынадай болады.
десек, онда мынадай болады.
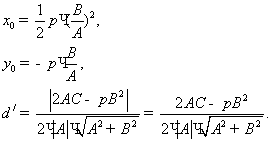
(мұндағы,![]() ;
; ![]() )
)
4 – теорема:![]() (
(![]() ) түзуіне дейінгі аралығы ең
қысқа болатын,
) түзуіне дейінгі аралығы ең
қысқа болатын, ![]() ; (
; (![]() ), параболасының бойындағы бір
нүктені
), параболасының бойындағы бір
нүктені ![]() деп, ал ең қысқа
аралықты
деп, ал ең қысқа
аралықты![]() десек, онда мынадай болады.
десек, онда мынадай болады.
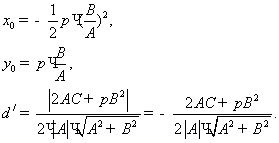
(мұндағы,![]() ,
, ![]() )
)
5 – теорема:![]() (
(![]() ) түзуіне дейінгі аралығы ең
қысқа болатын,
) түзуіне дейінгі аралығы ең
қысқа болатын, ![]()
![]() параболасының бойындағы бір
нүктені
параболасының бойындағы бір
нүктені ![]() деп, ал ең қысқа аралықты
деп, ал ең қысқа аралықты ![]() десек, онда мынадай болады.
десек, онда мынадай болады.
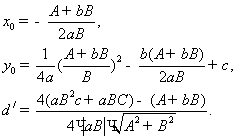
( Мұндағы ![]() ,
, ![]() )
)
Салдар:5 – теоремада, егер ![]() болса, онда мынадай болады.
болса, онда мынадай болады.
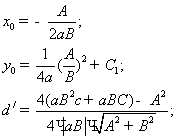
(Мұндағы ![]() болады.)
болады.)
![]() теоремалардың дәлелденуі 1 –
теоремының дәлелденуімен ұқсас (екі түрлі дәлелдеу
тәсілі болады) болғандықтан олардың дәлелелденуі
қалтырылды.
теоремалардың дәлелденуі 1 –
теоремының дәлелденуімен ұқсас (екі түрлі дәлелдеу
тәсілі болады) болғандықтан олардың дәлелелденуі
қалтырылды.
Енді жоғарыдағы теоремалар бойынша, мына
есептерді шешіп көрейік.
1-мысал:
(1)![]() түзуіне дейінгі аралығы ең
қысқа болатын,
түзуіне дейінгі аралығы ең
қысқа болатын, ![]() параболасының бойындағы бір
нүктені табайық?
параболасының бойындағы бір
нүктені табайық?
(2)![]() параболасының бойынан бір
нүкте табайық.Сол нүктеден
параболасының бойынан бір
нүкте табайық.Сол нүктеден ![]() түзуіне дейінгі аралық ең
қысқа болсын?
түзуіне дейінгі аралық ең
қысқа болсын?
Шешуі:
(1)![]() болғандықтан,
табылатын нүктені
болғандықтан,
табылатын нүктені ![]() десек,1- теорема бойынша мынау шығады.
десек,1- теорема бойынша мынау шығады.
![]()
![]()
Сондықтан ![]() болады.
болады.
(2)![]() болғандықтан, табылатын нүктені
болғандықтан, табылатын нүктені ![]() десек, 3-теорема бойынша
десек, 3-теорема бойынша
![]()
![]() шығады.
шығады.
Сондықтан іздеген нүкте ![]() болады.
болады.
2-мысал:![]() параболасының
бойындағы бір нүктеден,
параболасының
бойындағы бір нүктеден, ![]() түзуіне дейінгі ең
қысқа аралықты табайық?
түзуіне дейінгі ең
қысқа аралықты табайық?
Шешуі:![]() болатындықтан, 4-теорема
бойынша
болатындықтан, 4-теорема
бойынша ![]() мынаған тең болады.
мынаған тең болады.
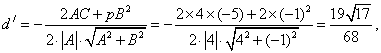
3-мысал:
(1) ![]() түзуіне дейінгі
қашықтығы ең қысқа болатын,
түзуіне дейінгі
қашықтығы ең қысқа болатын, ![]() параболасының бойындағы бір
нүктені табайық?
параболасының бойындағы бір
нүктені табайық?
(2) ![]() түзуіне дейінгі, аралығы ең
қысқа болатын
түзуіне дейінгі, аралығы ең
қысқа болатын
![]() параболасының бойындағы бір
нүктені табайық?
параболасының бойындағы бір
нүктені табайық?
Шешуі:
(1)![]() болатындықтан, табылатын
нүктені
болатындықтан, табылатын
нүктені![]() десек, 5-теорема бойынша мынау шығады.
десек, 5-теорема бойынша мынау шығады.
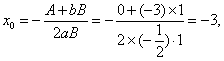
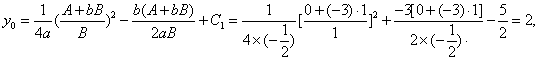
Сондықтан ![]() болады.
болады.
(2) ![]() болатындықтан, табылатын нүктені
болатындықтан, табылатын нүктені ![]() десек 5-теореманың салдары бойынша мынау
шығады.
десек 5-теореманың салдары бойынша мынау
шығады.
![]()
![]()
Сондықтан ![]() болады.
болады.
Жоғарыдағы
теоремаларды қолданғанда берілген парабола теңдеуі
қайсы түрдегі параболаның нормал (қалыпты) түрі
екендігіне, сонымен бірге берілген түзудің теңдеуі
сөзсіз түзу теңдеуінің жалпы түріне келтірілген
болуы қажет екендігін есте сақтап, есептерді шешуде оған
назар аудару керек. Сөзіміз дәлелді болуы үшін мына бір
есепті шешіп көрейік.
Мысалы: ![]() параболасының бойынан бір нүкте
табыңдар. Сол нүктеден
параболасының бойынан бір нүкте
табыңдар. Сол нүктеден ![]() түзуіне дейінгі аралық ең
қысқа босын?
түзуіне дейінгі аралық ең
қысқа босын?
Шешуі:Берілген парабола теңдеуін нормал
(қалыпты) түрге келтірсек ![]() болады. Бұл
болады. Бұл ![]() параболасы болып
параболасы болып ![]() болады.
болады.![]() теңдеуін түзу
теңдеуінің жалпы түріне
теңдеуін түзу
теңдеуінің жалпы түріне
келтірсек, ![]() болып,
болып, ![]() болады. Табылатын нүктені
болады. Табылатын нүктені![]() десек, 1-теорема бойынша мынау шығады.
десек, 1-теорема бойынша мынау шығады.
![]()
![]()
Сондықтан біз іздеген нүкте ![]() болады.
болады.
Әдебиеттер
1.Джанабердиева С.А. Шалбаев Е.Б., Ермекқызы Л.
Орта мектептегі бейінді математика сабақтарында дифференциалдық
теңдеулерді оқыту мәселелері / «Садықов оқулары»
– халықаралық ғылыми-теориялық конференция материалдары
– ҚазҰПУ, 2012. – 62-65 беттер.
2. Конфуций.
Избранные мысли и афоризмы // [Электрондық ресурс]. –
2012. – Сайттағы жету режимі: http://library.vladimir.ru/pisat_konfuc_2.htm
3. Әлімов А. Оқытудың интербелсенді
әдістемесі / Семинар-тренинг материалдары –ҚазҰПУ, 2012. – 23
бе