Физика /1.Теоретическая физика

Капаруллина А.И.

Государственный морской университет имени адмирала Ф.Ф.Ушакова,

Россия

Эффективная масса электрона в металле

Эффективная масса – это величина, имеющая размерность массы, характеризующая динамические свойства квазичастиц. Например, движение электрона проводимости в кристалле под действием внешней силы F и сил со стороны кристаллической решётки в ряде случаев может быть описано как движение свободного электрона, на который действует только сила F (закон Ньютона), но с эффективной массой , отличной от массы m свободного электрона. Это отличие отражает взаимодействие электрона проводимости с решёткой.

В кристалле свободному электрону необходимо составить группу волн де-Бройля с различными значениями частот и волновых векторов . Скорость перемещения центра такой группы соответствует скорости перемещения электрона в кристалле:

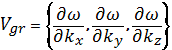
Решим задачу для одномерного случая. Под действием внешнего электрического поля растёт скорость, а, следовательно, и энергия, которая равна работе dA, которую совершает внешняя сила за бесконечно малый промежуток времени dt:

Так как

, то

Подставив данное выражение в (1), получим:

Уравнение (2) распространяется и на трёхмерный случай. Из данного выражения мы видим, что изменяется аналогично с импульсом в классической механике, поэтому называют квазиимпульсом электрона в кристалле. Найдём ускорение электрона:

Учитывая, что

Сравнивая выражение (3) со вторым законом Ньютона, приходим к выводу, что электрон движется под действием внешней силы F так же, как двигался бы свободный электрон, если бы он обладал массой. Следовательно, электрон проводимости можно рассматривать как квазичастицу.

Эффективная масса равна:

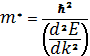
где,

ℏ — постоянная Планка, равная

k — волновая функция;

E — энергия электрона.

Эффективная масса может сильно отличаться от истинной массы электрона m, в частности она может принимать отрицательные значения. Введение эффективной массы позволяет, абстрагируясь от взаимодействия электронов с решёткой, определить характер движения электрона под действием внешнего поля. Приписав электрону массу , мы можем исследовать поведение электрона под действием силы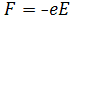, считая его свободным.

Понятие эффективной массы встречается в вопросе об электропроводности металлов, так как электроны проводимости в металле ведут себя как квазичастицы с эффективной массой электрона. Поэтому движение «среднего» электрона описывается уравнением вида:

где,

— средняя скорость свободных электронов, имеющихся в единице объёма металла, или дрейфовая скорость, (4), где n — концентрация.

— сила «трения», — коэффициент пропорциональности.

Если после установления стационарного состояния выключить внешнее поле (Е=0), то дрейфовая скорость начнёт убывать и по достижению состояния равновесия обратится в нуль.

Отсюда дрейфовая скорость равна:

— значение дрейфовой скорости в момент выключения поля.

— время релаксации, характеризующее процесс установления равновесия между электронами и решёткой.

Заменив r на в ходе вычислений, приходим к тому, что удельная электропроводность равна:

Выкладки, приведшие к формуле (5) справедливы как для классической, так и для квантовомеханической трактовки. Различие трактовок заключается в том, что при классическом рассмотрении предполагается, что все электроны возмущаются внешним электрическим полем, в соответствии с чем каждое слагаемое (4) получает добавку в направлении противоположном E, а при квантовомеханической трактовке приходится принимать во внимание, что коллективное движение электронов в поле воспринимается как возмущение полем лишь электронов, занимающих состояние вблизи уровня Ферми. Также в классической трактовке задействована истинная масса m, а при квантомеханической – эффективная масса

Научный руководитель: к.п.н., доцент С.А. Мищик

ЛИТЕРАТУРА:

Прохоров А.М. Физический энциклопедический словарь. — М.: Советская энциклопедия, 1983.

Савельев И. В. Курс физики, том 3, — М.: Наука, 1989.— С.184-189.

Паршин А.С. Электроны в твёрдых телах — Красноярск: САА, 1998 — Гл.2