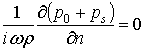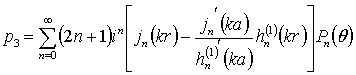Д.т.н., професор В.П. Нагорний, к.т.н. І.І. Денисюк, Юшицина Я.О.

Інститут геофізики ім. С.І. Субботіна НАН України

Розсіювання акустичної хвилі зерном

Процес взаємодії акустичних хвиль тиску з неоднорідностями (перешкодами) різної форми супроводжується розсіюванням хвиль і, як результат, в тій чи іншій мірі, зміною хвильового поля, як по амплітуді, так і по формі хвиль [1]. Відомі теоретичні дослідження таких процесів [1–4], проте чисельних розрахунків хвильових полів проведено недостатньо і вони виконані переважно для металів [4].

Нехай у геофізичному середовищі з параметрами ρ і с (де ρ, с – густина породи середовища і швидкість подовжньої хвилі в ній, відповідно) розміщена перешкода у вигляді жорсткого зерна сферичної форми. Розглянемо випадок, коли жорстке зерно радіусом не має можливості поворотів у середовищі, в якому поширюється падаюча на зерно плоска акустична хвиля з амплітудою р₀ і частотою ω

,

(1)

що взаємодіє з перешкодою (рис. 1).

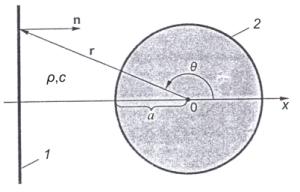
Рис. 1. Падаюча плоска хвиля на жорстке зерно:

1 – фронт падаючої плоскої хвилі; 2 – жорстке зерно

Розсіювання хвилі на перешкоді визначається значною мірою співвідношенням між довжиною падаючої хвилі та розміром перешкоди. Якщо розміри перешкоди значно менші ніж довжина падаючої хвилі, то в цьому випадку існує розв’язок для знаходження амплітуд розсіяного поля жорстким зерном. Коли ж розміри перешкоди великі порівняно з довжиною падаючої хвилі і поверхня перешкоди гладка, то знаходження розсіяного поля пов’язане з побудовою променевих зображень [1].

Розглянемо випадок, коли довжина падаючої хвилі λ і розміри зерна співрозмірні. Проведемо дослідження повного акустичного поля, що виникає в результаті розсіювання жорстким зерном сферичної форми падаючої акустичної хвилі виду (1).

Для ідеально жорсткої перешкоди на її поверхні складова швидкості частинок середовища дорівнює нулю () [1], тобто

,

(2)

де – амплітуда розсіяної хвилі.

З використанням граничної умови (2) в роботі [3] одержана залежність для визначення повного акустичного поля тиску навколо зерна радіусом a

,

(3)

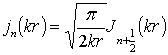де – уявна одиниця; – сферичні функції Бесселя; 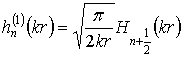– сферичні функції Ханкеля першого роду [5]; – хвильове число; – поліноми Лежандра; ; – похідні функцій ; в точці , відповідно; θ, r – координати точки середовища в полярній системі координат.

Використавши залежність (3), визначимо поле тиску навколо жорсткого зерна радіусом м, що знаходиться в пісковику з параметрами:  кг/м³;  м/с.

Падаюча хвиля має лінійну частоту  кГц. Хвильове число ; ; .

За приведеними параметрами визначено нормоване акустичне поле тиску для найбільш характерних напрямів і (рис. 2).

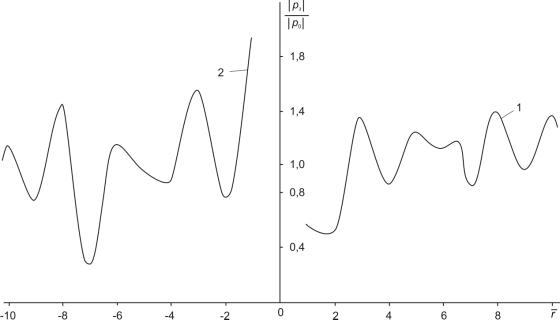
Рис. 2. Амплітуди повного акустичного поля на близьких відстанях від центра зерна: 1 – ; 2 –

З рис. 2 видно, що повне акустичне поле в досліджених напрямах має коливальний характер із наявністю максимальних значень на певних відстанях = від центра зерна.

Таким чином, наявність в геосередовищі жорсткого сферичного зерна в процесі поширення падаючої акустичної хвилі з амплітудою призводить до виникнення в середовищі розсіяної хвилі з амплітудою , суперпозиція якої з падаючою хвилею створює сумарне акустичне поле , амплітуда якого має коливальний характер і в розглянутих напрямах і перевищує амплітуду падаючої хвилі.

Література

1. Грінченко В.Т., Вовк І.В., Маципура В.Т. Основи акустики. – К.: Наук. думка, 2007. – 640 с.

2. Гузь А.Н., Кубенко В.Д., Черевко М.А. Дифракция упругих волн. – К.: Наук. думка, 1978. – 307 с.

3. Скучик Е. Основы акустики. – М.: Мир, 1976. – Т. 1. – 520 с; – Т. 2. – 542 с.

4. Горовенко А.П. Дифракція хвиль тиску на пружному сферичному включенні в пружному середовищі. – К., 2014. – 34 с. (Препр. / НАН України. Ін-т геофізики ім. С.І. Субботіна).

5. Справочник по специальным функциям / Под ред. М. Абрамовица, И. Стиган. – М.: Наука, 1979. – 830 с.