Айтбаева З.К.

Тараз мемлекеттік университеті, Казахстан

Кавитациялық аппаратта тамақ қалдықтарын органикалық бөлігін ұсақтау және араластыру әдісін математикалық моделдеу

Ақау қатты шекарасына оның конфигурациясы бойынша эллипстік нормаға жақын шектеу қойылады. Сұйықтағы транзиттік ағын әсерінің нәтижесінен ойықта айналу қозғалысы туындайды. Егер қатты және сұйық шекарасында туындайтын сұйық қозғалысының кедергісін есепке алмаса, онда бүтін қозғалыс көрсетілген геометриялық байланыстармен бірге шоғырлануы (тұйық траекторияда бірқалыпты айналу жылдамдығымен жүреді. Осындай козғалыс үшін қамтамасыз етуді эллипс траекториясы бойымен сұйық бөлшектерінің айналу жылдамдығы функциясы турінде көрсетеміз:

(1)

Айналу жылдамдыгының құраушылары Ох және Оу бойымен:

(1.1)

Координата осьтеріндегі эллипс траекториясымен сұйықтың бір қалыпты қозғалысының күшінің проекциясы:

(1.2)

Біріншіден қарастырылған каверндегі сұйық қозғалысы бірқалыпты емес, мұнда кавернде жиналған сүйықтың транзиттік ағынының энергиясының диссипациясы жүреді және тұтқырлық әсерінен туындайды және каверндегі сұйық қозғалысының ішкі кедергісінің күшін есептеу қажет. Кедергі күшін каверндегі сұйық қозғалысының жылдамдығына пропорционал етіп аламыз:

(1.3)

, Ох жэне Оу координат осінің бойындағы кедергі күштерінің құраушылары:

(1.4)

;

Екіншіден каверндегі сұйық пен транзиттік ағын арасындағы бөліну бетінде туындайтын кедері күші есептелуі қажет. Бұл күшті бөлу бетіндегі сұйық қозгалысының салыстырмалы функциясы түрінде жазамыз, оны транзиттік ағын мен сәйкес каверндегі бірқалыпты емес сұйық қозғалысының жылдамдығы арқылы бейнелейміз Ох осі бойымен:

(1.5)

Каверндегі сұйық бөлшектерінің қозғалысының динамикалық теңдеуін құрамыз, мұнда (m) массаны есептейміз:

(1.6)

жүйеге бұрын табылған күшпен оның проекциясының мәнін қоямыз:

(1.7)

тәуелділікті біртекті емес екінші ретті қарапайым дифференциалдық теңдеулердің сызықтық емес жүйесін көрсетеді, оның көмегімен каверндегі сұйықтың әр түрлі жағдайын тексеруге болады.

Оның аналитикалық шешімі едәуір қиындықты тудырады, сондықтан көрсетілген жағдайды талдау үшін жазылған теңдеулерді интегралдап, бірінші ретті дифференциалды теңдеулер жүйелерін шешуге келтіреміз, айнымалыларды орнына қоямыз:

(1.8)

Мұндай ауыстырулар жасаған соң теңдеуді келесі түрде жазамыз:

(1.9)

Каверндегі ортаны түрақты деп есептеп шекаралык шарттарын таңдаймыз:

(1.10)

Шешімін алу үшін айнымалы қадамды Булирша-Штерн әдісін колданамыз. Математикалық модель негізінде құрылған модельді талдау каверндегі гидродинамикалық жағдайда әсер ететін транзиттік ағын жылдамдығы мен сыртқы күштің кедергісі сияқты маңызды технологиялық параметрлерді бағалауға мүмкіндік береді. Жүйе теңдеулеріне енетін сандық коэффиценттерді эксперименталды нақтылау орталық тарту күші әсерінен материалдардың бұзылуы мүмкін гидродинамикалық режимді есептеуге мүмкіндік береді.

Шекаралық қабатты үзуді математикалық сипаттау.

Құбырдағы турбуленттік ағынды келесі теңдеумен сипаттаймыз

(1.11)

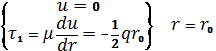
шекаралық мәндері кезінде теңдеуді тұтқыр қабат қалыңдығын есепке алмай жазамыз:

(1.12)

(1.22) интегралдап,шекаралық мәнін қойып, келесіні аламыз

(1.13)

мұндағы:

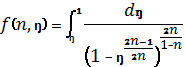
Қарастырылған модель жиегінде теңдей турбулентті шекаралық қабатты автомодельді деп есептейміз. Қабаттың сыртқы шекарасындағы жылдамдық келесі түрде беріледі

мұндағы - тұрақтылар

Өлшемсіз координата енгіземіз

мұндағы

(1.14)

=const (1.15)

Жеңілдетіп орындарына қойған соң Фоннер және Скэн теңдеулерін аламыз:

(1.16)

(1.16) теңдеудің сандық шешімін аламыз, оған жоғарғы ретті дифференциялдық теңдеулерді бірінші ретті дифференциалдық теңдеулер жүйесіне келтіреміз.

Субстрат тамшысының динамикалық ұшуын математикалық сипаттау.

Әртүрлі факторлардың (ағынның жылдамдығы, шығыны, беттегі қасиеті Органикалық субстраттың физикалық-химиялық параметрлері, компоненттердің жылулық -физикалық қасиеттері температуралық режимі,

құрамдас бөліктерінің дисперсиясы бір-біріне өзара әрекеттесуі және әсері, олардың сандық есепке алуын кажет етеді, органикалық субстратты дайындау және ұсату үрдістерді математикалық модельдеу әдістерін пайдалану арқылы іске асырылады.

Форсункамен сұйық субстраттың тозаңдануы кезінде тамшы спектрі Розин-Раммлер үлестіру функциясымен сипатталынады. Розин-Раммлер бойынша фракционды үлестірілуінің интегралды функциясы келесі түрде келтірілген:

(1.17)

Мұндағы

R – d -дан үлкен диаметрге ие болатын тамшылардың өлшемдік сипаттамасы;

d₀ - тамшылардың өлшемдік сипаттамасы; n - үлестіру гұрақтысы.

Тәжірибеллік мәліметтерге сәйкес, механикалық және паромеханикалық форсункалар үшін n -2-ден 4-ке дейін өзгереді. Статистикадағы жалпы қабылданған d_i шамасы 0,27% ықтималдылығын құрайтын шектеулікті ұсынады. Яғни “mах”, “mіn” тамшылардың диаметрі үлестіру қисығының нүктесіне сәйкес келеді. “R” ординаталары 0,27 және 99,73% тең. Осыған сәйкес тамшылардың mах және mіn диаметрлері төмендегідей есептелінеді:

(1.18)

(1.19)

Есептеуде тамшылардың өлшемді сипаттамасында үлкен диаметрі тамшы алынды. Сонда (3.27) теңдеу сипаттау өлшемін максимумге алмастырып, мына теңдеуді аламыз:

(1.20)

Мысалы жасалған тамшы ұсатқаннан соң бірінші сатыда шар тәріздес формада болады. Онда шар тәріздес тамшының қозғалысының теңдеуі оның бетіне әсер ететін тепе тең күштерін көрсетеді

(1.21)

Газ жағынан тамшыға әсер ететін “Ф” кедергі күші:

Декарттық координат жүйесінде берілген теңдеудің проекциясы үшін келесіні жазуға болады:

Алынған нәтижелерді талдау шекаралық қабатты түзу жоғары қалыпты кернеудің туындауына және материалдардың бұзылу нәтижесінде каверннің пайда болуын көрсетеді және шикізатқа кавитациялық сипатта әсер етуді тәжірибелік жүргізу келесі қорытындыларды жасауға мүмкіндік береді:майдаланатын компоненттердің құрылымдык -механикалық қасиеттерін және құрамын білу қажет.