Технические науки / 5. Энергетика

Магистрант Сагатов А.Р., к.т.н. Тулегенов К.К.

Западно-Казахстанский аграрно-технический университет им. Жангир хана, Казахстан

Математическая модель сближения фазных проводов сельских ВЛ 6-10 кВ при воздействии ветра

Известные модели сближения проводов и методы определения расстояний между проводами основываются на изучении перемещений одиночного провода под действием ветра и не учитывают аналитическую связь между взаимными перемещениями проводов. В работе В. В. Бургсдорфа [1] отмечено, что взаимное экранирование проводов соседних фаз не имеет место, а расстояния между ними не столь велики, чтобы можно было допустить различные условия распространения воздушного потока. Поэтому при одинаковых стрелах провеса следует ожидать близких к синхронным колебаний проводов и сближения между ними возможны лишь при разных условиях колебаний отдельных проводов. Одним из таких условий является неравенство стрел провеса фазных проводов. Оно может возникать в процессе эксплуатации из-за удлинения провода или ослабления его крепления к штыревому изолятору. На ВЛ 6-10 кВ имеющих, в отличие от ВЛ 35 кВ и выше, малые длины пролетов и стрелы провеса проводов, даже небольшое неравенство длин фазных проводов в пролете вызывает значительную относительную разрегулировку их стрел провеса. Это, в свою очередь, оказывает существенное влияние на несинхронность их взаимных перемещений, так как в зависимости от величины стрел провеса проводов изменяются их частотные и демпфирующие характеристики.

В известных моделях оценка сближений проводов проводится только для середины пролета. Теоретические исследования показали, что при несинхронных раскачиваниях проводов ВЛ 6-10 кВ с разными стрелами провеса опасные сближения могут возникать не только в середине пролета, но и в других местах по его длине. Это подтверждается практикой: повреждения проводов В Л 6—10 кВ при ветре, как отмечалось при анализе аварийных отключений, наблюдаются на разных участках проводов по длине пролета. Сближения фазных проводов в пролете ВЛ происходят при порывистом характере воздействующего ветрового потока. Такое воздействие можно представить в виде последовательности порывов ветра с разными паузами (промежутками) между ними. При таком подходе, как отмечается в работах [2,3], наибольшие сближения проводов могут возникать в периоды этих пауз. Поэтому при моделировании будем рассматривать взаимные перемещения двух проводов в пролете с разными стрелами провеса в периоды пауз между порывами ветра. Из-за неодновременности воздействия скоростных напоров, обусловленных порывами ветра, разные части провода в пролете, как указывается в работе [4], будут находиться в различных фазах движения. Поэтому суммарное отклонение провода определяется не максимальной скоростью, а ее усредненной величиной. Будем считать, что при воздействии' ветра провода отклоняются на определенный угол , а во время паузы между порывами совершают свободные затухающие маятниковые колебания (раскачивания). При этом существенное значение имеет соотношение между периодами раскачиваний проводов и продолжительностью пауз между порывами ветра. В работе [5] отмечается, что несинхронные колебания и схлестывания проводов возможны в паузах между порывами ветра, когда периоды их раскачиваний менее 5 секунд. На ВЛ 6—10 кВ-с малыми стрелами провеса проводов периоды раскачивания могут оказаться меньше паузы между порывами ветра, при этом провода будут сближаться на опасные в изоляционном отношении расстояния.

Ветровая нагрузка в даН определяется по формуле, рекомендованной Правилами устройства электроустановок (ПУЭ):

где: — коэффициент, учитывающий неравномерность скоростного напора ветра по пролету ВЛ;

— коэффициент, учитывающий влияние длины пролета на ветровую нагрузку;

— коэффициент лобового сопротивления;

— нормативный скоростной напор ветра, даН/м ;

F — площадь диаметрального сечения провода, м2;

— угол между направлением ветра и осью ВЛ.

Угол отклонения провода от вертикали 0 определится приложенными к

нему силами, т.е.

(1)

где: V - скорость ветра, м/с;

G - вес провода в пролете, даН.

Рассмотрим пролет В Л 6-10 кВ с треугольным расположением проводов на опорах с расстояниями a и b соответственно по горизонтали и вертикали и

стрелами провеса проводов . Предположим, что каждый колеблющийся провод является плоской кривой, расположенной во вращающейся вместе с проводом плоскости, проходящей через точки подвеса. Расчетная схема для определения расстояний между проводами в вертикальной плоскости, перпендикулярной оси пролета, на расстоянии х от опоры представлена на рисунке 1. Выразим координаты точек тәуелді , которые изменяются во времени в системе координат zOy [4]:

где: — величины провеса проводов на расстоянии х от точек крепления;

, – функции изменения углов отклонения проводов от времени при их маятниковых колебаниях.

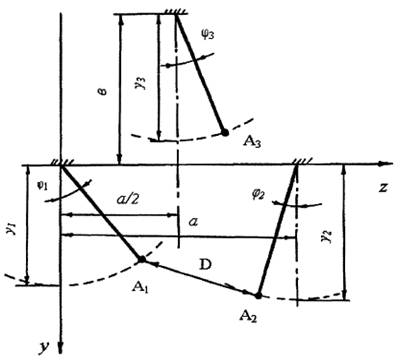
Рисунок 1. К определению расстояний между проводами

при их несинхронных маятниковых колебаниях

Определим закон изменения расстояний между двумя колеблющимися фазными проводами, расположенными, например, горизонтально, т.е. сведем задачу к расчету расстояний между двумя точками и с изменяющимися во времени координатами: Функцию изменения расстояний между проводами, от времени определим следующим образом:

(2)

После соответствующих преобразований формулы (2) получим

(3)

Будем считать угол отклонения провода от положения равновесия против часовой стрелки положительным, по часовой — отрицательным. Аналогично можно определить расстояния между точками и :

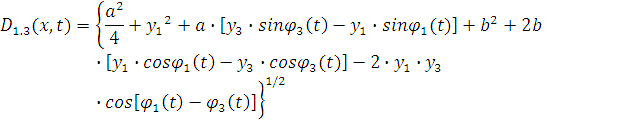
Из выражения (3) видно, что расстояние между колеблющимися в пролете проводами зависит от соотношения стрел провеса фазных проводов, т.е. степени их разрегулировки и закона маятниковых колебаний проводов. При равенстве стрел провеса и идентичности характеристик ветрового потока по формуле (3) т.е. подтверждается синхронное раскачивание проводов.

Согласно исследованиям А. А. Макарова [5], Ю. И. Горошкова и А. И. Гукова [2] при маятниковых раскачиваниях провода величина его смещения, от положения равновесия в любой момент времени определяется начальным углом, отклонения , частотой маятниковых раскачиваний величиной затухания . На основе теоретических и экспериментальных исследований угловые отклонения провода при маятниковых колебаниях в любой момент времени паузы между порывами ветра определятся следующим образом:

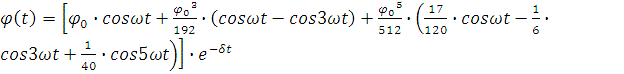(4)

Таким образом, моделирование взаимных перемещений двух фазных проводов с разными стрелами провеса в пролете ВЛ 6—10 кВ при их маятниковых колебаниях во время пауз между порывами ветра осуществляется путем использования полученной нами формулы (3) и выражений (1), (4). После подстановки и соответствующих математических преобразований, процесс изменения расстояний между двумя фазными проводами при их маятниковых колебаниях с учетом коэффициента разрегулировки стрел провеса может быть представлен в общем виде:

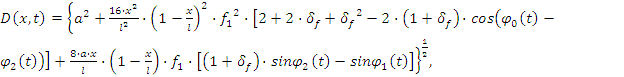(5)

На основе разработанной математической модели выполнены на ПК численные расчеты расстояний между проводами в каждый момент времени их маятниковых колебаний в любой части длины пролета при разных параметрах ветрового воздействия и степени разрегулировки фазных проводов.

Анализ результатов расчета позволяет определить время, в течение которого возникают опасные сближения проводов в процессе их несинхронных, маятниковых колебаний. Важное практическое значение имеют зависимости минимальных расстояний, между проводами от скорости ветра при разных коэффициентах разрегулировки стрел провеса.

Литература

1. Бургсдорф В.В. Новые исследования в области линий электропередачи / В.В. Бургсдорф // Воздушные линии электропередачи: переводы докладов Международной конференции (СИГРЭ) - М. : 1965.- С. 3-28.

2. Горошков Ю. И. Ветроустойчивость контакной сети / Ю. И. Горошков, А.И. Гуков. – М.: Транспорт, 1969. – 128 с.

3. Кабашев В.Ю. Повышение надежности сельских воздушных линий 6-10 кВ в условиях воздействия ветровых нагрузок: монография / В.Ю. Кабашев.- Уфа: Изд-во «Здравохранение Башкортостана», 2009. – 140с.

4.Крюков К.П. Конструкции и расчет опор линий электропередачи / К.П. Крюков; А.И. Курносов, Б.П. Новогорцев. – М.; Л. : Энергия; 1964. – 586с.

5. Макаров А.А. Затухание колебаний проводов воздушных линий электропередачи / А.А. Макаров // Надежность и долговечность строительных конструкций. – Волгоград, 1974. – С. 144 – 146.