К.ф.-м.н. Докукова Н.A., к.ф.-м.н. Конон П.Н.

Белорусский государственный университет, Минск, Беларусь

Исследование колебаний n - автономных осцилляторов на подпружиненной платформе с внешним затуханием

Множество одинаковых горизонтально колеблющихся элементов с внешним затуханием зафиксированы на подпружиненной платформе с амортизаторами, обеспечивающими вязкое трение. Математическая модель движений всех тел механической системы сформирована из линейных неоднородных дифференциальных уравнений по динамической схеме [1] и в каноническом виде динамической модели [1 - 4]

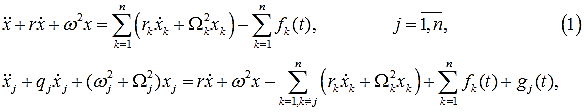
где − перемещения масс ; − собственные и парциальные частоты платформы и осцилляторов; − коэффициенты упругости пружин; r =b/M , r_j =b_j/M, q_j=(1/M+1/m_j) – относительные величины, в которых b и b_j коэффициенты демпфирования соответствующих амортизаторов; f_j =F_j/M и g_j F_j/m_j – приведенные силы .

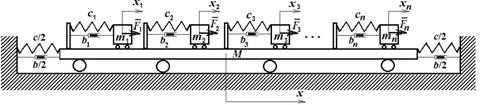
Рисунок 1 - Схема движений n - метрономов на колеблющейся горизонтальной платформе

Для упрощения расчетов положим, что все собственные и парциальные частоты n элементов одинаковы , , тогда корни характеристического уравнения примут вид на основании условий устойчивости по Воронову В.С. многоэлементной динамической системы. К системе уравнений движения (2) необходимо присоединить начальные условия для ее полного разрешения:

, , . (2)

Законы движений многоэлементной модели (1) таковы:

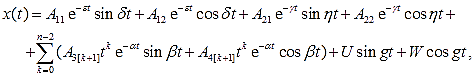(3)

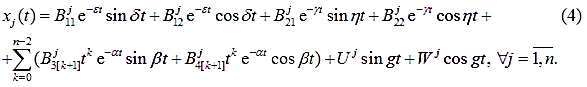
В этих формулах коэффициенты и , остальные имеют громоздкий вид и по этой причине здесь не приводятся. Относительно них можно высказать общие замечания, при которых в динамической системе будет наблюдаться синфазные либо противофазные колебания. Например, колебания , будут синфазными, если все коэффициенты будут пропорциональны друг другу с одной и той же величиной пропорциональности одновременно , рисунок 2.

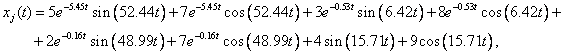(5)

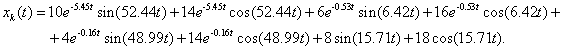(6)

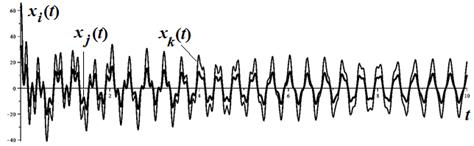
Рисунок 2 - Синфазные движения и двух автономных осцилляторов на подпружиненной платформе с внешним затуханием при

Противофазными станут движения, если все коэффициенты будут пропорциональны друг другу с одним и тем же отрицательным значением одновременно , рисунок 3.

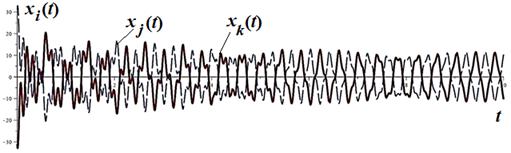
Рисунок 3 - Противофазные движения и двух осцилляторов при

Литература:

1. Dokukova N.A., Kaftaikina E.N., Konon N.P Investigation of sets synchronization of movements oscillator with zero initial conditions// MISPC XI «Conduct of modern science». Mathematics. Modern information technologies. Sheffield. Science and Education Ltd. Velocity Tower, Sheffield, S Yorkshire, England.− V. 22. − 2015. −P. 7-14.

2. Dokukova N.A., Kaftaikina E.N. Natural oscillations synchronization of multi-element-dynamical system of autonomous oscillators // MISPC XI «Conduct of modern science − 2015». Technical sciences. Science and education.- Sheffield, S Yorkshire, England.− V. 23. − 2015. P. 17-22.

3. Dokukova N.A., Kaftaikina E.N., Zenkovich V.V. // General patterns of improper vibrations of dynamical systems with an arbitrary number of degrees of freedom/ МНПК «Новины на научния прогрес -2011».– София: Бял ГРАД-БГ ООД.- 2011.– .Т. 9. – С. 56 – 64.

4. Dokukova N.A., Kaftaikina E.N., Konon N.P. N sync metronomes on a vibrating horizontal platform// MISPC XIII «Cutting-Edge Science - 2017». Mathematics.- Sheffield, S Yorkshire, England.− V. 5.− 2017.- P. 38-43.