С. М. Андрійко, О. О. Юрко

Кременчуцький національний університет імені Михайла Остроградського, Україна

Модернізація математичної моделі механізму генерування дихальних шумів

Дихальна система займає основне місце серед інших систем людського організму, забезпечуючи киснем організм людини, порушення роботи якої викликає зміну функціонального стану її органів, і відображується в дихальних шумах (ДШ). Тому, важливою медичною та технічною задачею є моделювання ДШ, як звуку дихання людини, що є актуальною науково-технічною задачею, розв’язання якої дає змогу зменшити економічні, часові та технічні витрати на проведення експериментів. Тому, обґрунтування математичної моделі дихального шуму, адекватної для задач діагностування дихальної системи людини, і методів його опрацювання для підвищення об’єктивності поставленого діагнозу є актуальною науковою задачею.

Метою роботи є удосконалення математичної моделі дихального шуму та розроблення методів його аналізу для підвищення інформативності діагностичних систем.

На найпростішої двовимірної фізичної моделі [1, 2] показано, що описаний механізм трансформації періодичних деформацій розтягування альвеол в поперечні коливання їх стінок можливий. Оскільки h << L, то замість реальної стінки цілком допустимо взяти прямокутну мембрану, закріплену по контуру (рис. 1). Нехай є деяке постійне яке залежить від часу натяг мембрани F₀ і невелике в порівнянні з розмірами мембрани початковий поперечний відхилення А(0) її центру в момент часу t = 0. Далі було проведено вплив на мембрану періодичним натягненням F(t), що імітує натяг, яке призводить до періодичного розтягування стінки альвеоли під час акту дихання, і подивимося, чи виникнуть при цьому поперечні коливання.

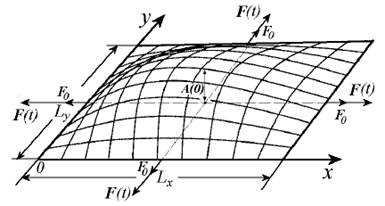
Рисунок 1 – Схема закріпленої по контуру мембрани в момент часу t = 0 [2]

Для того щоб вирішити цю задачу, було використано відоме диференціальне рівняння коливань мембрани, приведене до вигляду [2, 3]:

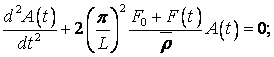(1)

де , , – поверхнева щільність матеріалу мембрани, , 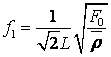– перша власна частота, F(t) – змінна складова натягу мембрани, що моделює натяг, що впливає на стінки альвеоли в процесі дихання, яка підпорядковується періодичному закону [2, 3]:

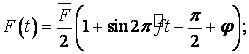(2)

де – фіксована частота, обчислена для періоду 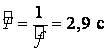, що приблизно відповідає реальній тривалості одного циклу вдих-видих; φ – початкова фаза; – амплітуда. Зауважимо, що функція F(t) позитивна при будь-яких значеннях t.

Рівняння (1) є однорідним диференціальним рівнянням другого порядку зі сталими коефіцієнтами, яке у загальному виді має вигляд:

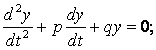або (3)

де 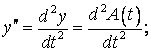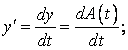y = A(t); p = 0; 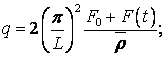кінцевий розв’язок якого має вигляд:

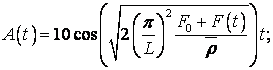(4)

при початкових умовах , .

Задавши параметри F₀, , L і φ, використовуючи вираз (11), отримаємо графік розподілу коливань альвеоли у часовій області, який наведено на рис. 2.

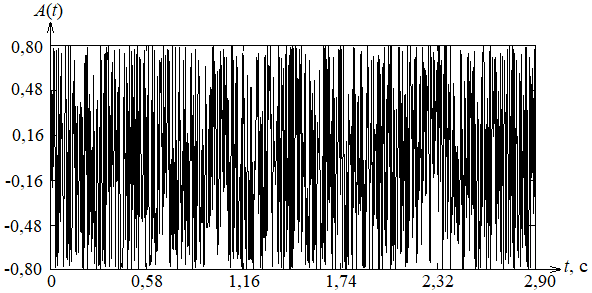
Рисунок 2 – Графік розподілу коливань альвеоли (для одного такту дихання)

Варто відзначити, що величина визначається із виразу 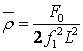при f₁ = 100 Гц і F₀ = 2 · 10^-5 Н/м.

Перевірка адекватності отриманих результатів проводилась у декілька етапів:

1. Визначення експериментальних точок. Для виконання умови підпорядкованості нормальному закону (виконання даної умови надасть можливості застосовувати стандартні статистичні методи обробки експериментальних даних) кількість експериментальних точок повинно бути не менше 33.

2. Побудова регресійної моделі (рівняння регресії), використовуючи метод найменших квадратів (лінійна, квадратична, параболічна, гіперболічна, показникова тощо).

3. Визначення коефіцієнтів кореляції, детермінації, середньої помилки апроксимації, фактичного (розрахованого) значення F-критерію Фішера та порівняння його з табличним.

За результатами статистичного аналізу отримані наступні показники:

– рівняння регресії;

r_xy = 0,954 – коефіцієнт кореляції, за яким щільність лінійного зв’язку між змінними може бути оцінена на підставі шкали Чеддока як вельми висока;

= 0,910 – коефіцієнт детермінації, який показав, що значення змінної у на 91,0 % залежить від х, тобто отримане рівняння регресії значиме.

= 1,097 % – середня помилка апроксимації, яка складає менше 10 %, що вказує на виску якість побудованої моделі.

Побудована модель є адекватною за критерієм Фішера, оскільки F_факт = 9,242, а табличне – F_табл(α; k₁; k₂) = 19,5 при рівні значимості α = 0,05 та числа ступенів свободи k₁ = 1 і k₂ = 33.

Література

1. Вовк И. В. Природа шумов дыхания и их мультифрактальные свойства / И. В. Вовк, В. Т. Гринченко, В. Т. Мацыпура //Акустический журнал. – 2013. – 59, № 5. – С. 636–647.

2. Вовк И. В. Моделирование механизма генерации везикулярных шумов дыхания / И. В. Вовк, В. Т. Мацыпура //Акустический журнал. – 2015. – Т. 17, № 1. – С. 17–22.

3. Гринченко В. Т. Основы акустики / В. Т. Гринченко, И. В. Вовк, В. Т. Мацыпура. – К. : Наук. думка, 2007. – 640 с.