Преобразование тригонометрических выражений

Тригонометрические задачи одна из самых сложных тем в школьном курсе математики. Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях.

Целью исследования данной работы является выполнение заданий на тождественные преобразования тригонометрических выражений, поскольку они встречаются в ЕГЭ как в качестве отдельных заданий, так и используются для решения тригонометрический уравнений и неравенств, а так же комбинированных заданий.

Проблема исследования состоит в рассмотрении теоретических основ темы «Преобразование тригонометрических выражений» и методики обучения решению таких типов задач.

Цель исследования: рассмотреть различные способы и методы решения тригонометрических выражений.

Выражение, в котором переменная содержится под знаками тригонометрических функций, называют тригонометрическим. Для преобразования выражений используют свойства тригонометрических функций и формулы тригонометрии.

Формулы сложения и вычитания аргументов. Для любых действительных чисел и справедливы формулы:

(1)

(2)

(3)

(4)

(5)

(6)

Формула (5) верна при отличных от Формула (6) верна при отличных от

Пример 1. Вычислить

Решение. Имеем Воспользовавшись формулой (3) при получим:

Известно, что . Значит

Итак,

Пример 2. Найти если

Решение. Воспользуемся формулой (5) и учтем, что

Имеем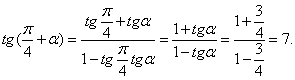

Формулы приведения. Под формулами приведения обычно понимают формулы, сводящие значение тригонометрической функции аргумента вида к функции аргумента [12, с.342].

Пусть, например, нужно вычислить Тогда имеем: .

Аналогично

Подобным же образом выводятся и остальные формулы приведения, эти формулы даны в следующей таблице:

Таблица 1

Формулы приведения

Функция	Аргумент
				-	-	-	-
		-	-	-	-
		-	-			-	-
		-	-			-	-

Соотношения между тригонометрическими функциями одного и того же аргумента. Если в формуле (2) положить то получим:

(6)

Откуда, в свою очередь, находим, что

(7)

(8)

Тождество (7) справедливо при а тождество (8) — при .

Равенства (6), (7), (8) связывают между собой различные тригонометрические функции одного и того же аргумента. Известны еще два равенства, связывающие между собой различные тригонометрические функции одного и того же аргумента. Это

и

Перемножая эти равенства, получаем равенство справедливое при

Формулы двойного угла. Если в формулах (3), (1), (5) положить то получим следующие тождества [4, с.231]:

(9)

(10)

(11)

С помощью формул (9), (10) и (11) можно выразить синус, косинус, тангенс любого аргумента через тригонометрические функции вдвое меньшего аргумента. Например, справедливы следующие равенства:

В ряде случаев полезным оказывается использование полученных формул (справа налево), то есть замена выражения выражением (или выражения выражением ), выражения выражением и, наконец, выражения выражением

Пример 3. Упростить выражение

Решение.

Литература:

1. Асмолов, А.Г. Математика в школе / А.Г. Асмолов – М.: Просвещение, 2016.

2. Блох, А.Я. Методика преподавания математики в средней школе: Частная методика: учеб. пособие для студентов пед. ин-тов по физ.-мат. спец. В.И.Мишин – М.: Просвещение, - 2017. – Гл. 5.

3. Виленкин, Н.Я. Равенства, тождества, уравнения, неравенства / Н.Я. Виленкин – М.: Просвещение, – 2016. – 271 с.

4. Макарычев, Ю.Н. Алгебра: учеб. для 8 кл. общеобразоват. учреждений / С.А. Теляковский – М. : Просвещение, 2015. - 271 с.