технические науки/ 2. транспорт.

Прокопенко В.С., студент 3-го курса Мартынов С.В.

Белгородский государственный технологический

университет им. В.Г. Шухова, Россия

Расчет ортотропных пластин и оболочек с низкой сдвиговой жесткостью на териосиловое воздействие

Представляет интерес анализ напряженно-деформированного состояния оболочечных конструкций композиционных анизотропных материалов с низкой сдвиговой жесткостью. К числу таких материалов относятся, например, органопластики. Для однонаправленных органоэпоксикомпозитов, относящихся к органопластикам, физические характеристики материала имеют следующие значения [1,5,6]: модули упругости ; модули сдвига коэффициент Пуасона; коэффициенты теплового линейного расширения =-3,5, =-35. При этом выполнение известное соотношение .

Упругие деформации для ортотропного материала определяются по формулам:

-- (1)

Компоненты напряженного состояния связываются с компонентами упругой деформации соотношениями:

(); (); (2)

Поставим в выражение для потенциальной энергии деформации формулы (1) и (2) и выполним интегрирование по нормальное координате z от -h/2 до h/2. В результате ряда преобразований получим:

U(v)=++ (3)

Усилия , … , , действующие в пологой ортотропной оболочке и входяшие в формулу (2), определяют по формулам:

+;

+;

+;

+;

(4)

Температурные усилия ,. и функции , определяются для изотропного материала соотношениями:

=+)

=+)

=+) (5)

=+)

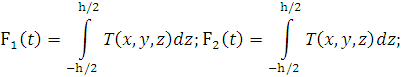
Учитывая, что

(+) ;

(+) ;

И отбрасывая в (3) чисто температурное слагаемое получим двумерный функционал теории оболочек, представляющий собой полную потенциальную энергию системы:

П(,q,v), (6)

где v=(,w- вектор, компонентами которого являются функции перемещений;

=(, ,,,,,,-вектор, компонентами которого являются составляющие тензора деформаций;

N=(, ,, ,,,,- вектор, компонентами которого являются усилия, определяемые по соотношении теории ортотропных оболочек (4);

=( 0 0 0 - вектор, компонентами которого являются температурные усилия, определяемые зависимости (5);

q=,, – вектор внешней нагрузки, компоненты которого имеют направления, соответствующие компонентам вектора перемещений.

Решение температурной задачи выполнилось методом конченых элементов, а определение напряженно-деформированного состояния пластин и оболочек выполнялось с помощью квазиньютоновского метода Дэвидона-Флетчера-Пауэлла [2,3,4] на основе функционала (6).

Рассмотрена пологая цилиндрическая оболочка из органопластика с физическими характеристиками, приведёнными выше.

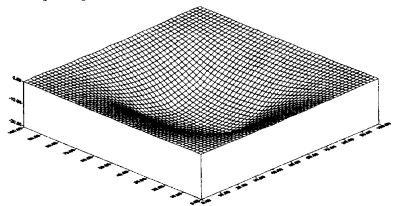
Рис.1. Прогибы w квадратной жестко закрепленной по контуру ортотропной пластинки

Оболочка имеет жесткое закрепление по криволинейным сторонам прямолинейные кромки свободны от закрепления. Геометрические параметры имеют следующие значения: размеры в плане a=b=1 м: толщина h=м; кривизны =0; =0,2 . Выполнен ряд расчетов оболочки при действии поперечной по объёму температуры Т=0; 20; 40; 60 град. При действии только поперечной нагрузки w направлены к центру кривизны оболочки.

Литература

1.Композиционные материалы: Справочник/ Под общ. Ред. В.В.Васильева, Ю.М. Тарнопольского-М; Машиностроение,1990-512с.

2.Анюхин Н.Н. Трушин С.И. Прилипов Н.В. Решение задач термоупругост оболочек методом прямой минимизации энергии.-строительная механика инжнерноых конструкций и сооружений№1 2005,с.99-102.

3. Прокопенко В.С., Шарапов Ринат Р., Агарков А.М., Шарапов Р.Р. Оптимизация работы оборудования для получения тонкодисперсных порошков // Вестник БГТУ им. В.Г. Шухова. 2015. № 1. С. 80-83.

4. Романович А.А. Особенности процесса постадийного измельчения материалов с использованием пресс-валкового агрегата// Известия высших учебных заведений. Строительство. 2007. № 9. С. 88-91.

5. Sharapov R.R., Prokopenko V.S. Modeling of the separation process in dynamic separators // World Applied Sciences Journal. 2013. Т. 25. № 3. С. 536-542.

6. Романович А.А., Орехова Т.Н., Мещеряков С.А., Прокопенко В.С. Технология получения минеральных добавок // Вестник БГТУ им. В.Г. Шухова. 2015. № 5. С. 188-192.