технические науки/ 2. транспорт.

Орехова Т.Н., студент 3-го курса Бабкин М.С.

Белгородский государственный технологический

университет им. В.Г. Шухова, Россия

Анализ методики расчета напор и подача гидравлического двигателя-насоса

Гидравлический двигатель-насос (в дальнейшем насос) работает с использованием возобновляемого источника открытых водных потоков. Он относится к группе объемных насосов.

Основанием для проектирования и гидравлического расчета насоса является проектное задание потребителя (заказчика) с указанием подачи насоса и геодезической высоты , м.

Уравнение баланса сил, обеспечивающих работу насоса, имеет вид:

(1)

где - сила Архимеда, Н; G - сила тяжести поршня с рабочей камерой, Н;

- сила трения в уплотнении, Н; - полезная часть силы Архимеда, расходуемая на вытеснение воды из рабочей камеры в нагнетательный трубопровод, Н.

, (2)

, (3)

, (4)

где - плотность воды, кг/; g - ускорение свободного падения, ;

- объем поршня с рабочей камерой, ; - средняя плотность поршня с рабочей камерой, кг/; f - коэффициент трения; l -длина уплотнения, м; р - давление рабочей жидкости, Па; d - диаметр в уплотняемом месте, м.

Из уравнения (1) полезная часть силы :

(5)

При этом давление в рабочей камере:

, (6)

где - живое сечение отверстия нагнетательного клапана, .

Применяя уравнения Бернулли и используя известную формулу для определения расхода жидкости через отверстие ( в данном случае отверстие нагнетательного клапана) при наличии противодавления , выразим напор насоса (2-3):

, (7)

где - коэффициент расхода нагнетательного клапана.

В уравнении (7) значение представляет собой напор насоса при заданных характеризует потери напора при перемещении воды через отверстие нагнетательного клапана, т.е.

, (8)

где h - напор насоса, м; - потери напора, м;

Таким образом, уравнение (8) представляет собой известное в гидравлических машинах определение напора насоса.

В зависимости от диаметра рабочей камеры и давления, которое развивается в ней, по справочным данным выбирается сальниковое уравнение (5). Тогда уравнение (1) при известных значениях можно представить как

. (9)

С учетом уравнений (2)-(3) после ряда преобразований имеем:

, (10)

При известном значении , - диаметр и высота поршня, м; - средняя плотность поршня с рабочей камерой, ; - плотность воды, .

Среднюю плотность найдем по формуле:

, (11)

где - масса поршня с рабочей камерой, кг.

Оптимальное соотношение определится в процессе экспериментальных исследований. В качестве аналога примем соотношение , , используемое для автомобильных карбюраторных двигателей (6). В общем случае при , . Подставив это соотношение в уравнение (10), найдем диаметр поршня:

, (12)

При известном значении можно определить , необходимых для расчета насоса.

Из условий работы насоса ход поршня Sне может быть больше высоты поршня, при сальниковое уплотнение выходит из обоймы рабочей камеры. Увеличение высоты приведет к повышению высоты напорного сооружения и капитальных затрат на строительство. Изменение S связано с изменением диаметра рабочей камеры, так как её высота . Соотношение подлежит определению после проведения экспериментов.

Объем и диаметр рабочей камеры возможно определить из условия равенства времени рабочего хода при заполнении цилиндра и вытеснении воды из рабочей камеры. Таким образом:

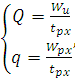(13)

где Q - расход воды при заполнении цилиндра на величину хода поршня S, ; q - подача насоса, ; - объем рабочей камеры, ; - объем рабочей камеры, .

Из условий системы управлений (13) после математических преобразований имеем:

. (14)

где - диаметр рабочей камеры, м; - диаметр цилиндра, м.

Примем отношение , тогда , или

(15)

Величина кольцевого зазора между цилиндром и поршнем зависит от материала стенок цилиндра (сталь, чугун, железобетон и др.) и соосности цилиндра с поршнем. Для стального цилиндра достаточно 10-15 мм.

Литература

1. Мелихов С.В., Прокопенко В.С. Анализ методики определения эффективности разделения // Инновационные материалы, технологии и оборудование для строительства современных транспортных сооружений Белгородский государственный технологический университет им. В.Г. Шухова. 2013. С. 143-147.

2. Орехова Т.Н., Прокопенко В.С. Тонкодисперсные порошки для асфальтобетона // Научный альманах. 2016. № 1-1 (15). С. 465-467.

3. Прокопенко В.С., Шарапов Ринат Р., Агарков А.М., Шарапов Р.Р. Оптимизация работы оборудования для получения тонкодисперсных порошков // Вестник БГТУ им. В.Г. Шухова. 2015. № 1. С. 80-83.

4. Романович А.А. Особенности процесса постадийного измельчения материалов с использованием пресс-валкового агрегата// Известия высших учебных заведений. Строительство. 2007. № 9. С. 88-91.

5. Sharapov R.R., Prokopenko V.S. Modeling of the separation process in dynamic separators // World Applied Sciences Journal. 2013. Т. 25. № 3. С. 536-542.

6. Романович А.А., Орехова Т.Н., Мещеряков С.А., Прокопенко В.С. Технология получения минеральных добавок // Вестник БГТУ им. В.Г. Шухова. 2015. № 5. С. 188-192.