технические науки/ 2. транспорт.

Прокопенко В.С., студент 3-го курса Бабкин М.С.

Белгородский государственный технологический

университет им. В.Г. Шухова, Россия

Анализ методики расчета давления давления между балкой и опорными пластинами, приваренными к колоннам

В статье решена контактная задача о взаимодействии свободно опертой железобетонной балки с опорной пластиной. Рассмотрен случай загружения балки с опорной стальной пластиной. Рассмотрен случай загружения балки равномерно распределенной нагрузкой.

Решим эту же контактную задачу, когда балка загружена сосредоточенной силой, приложенной в пролете в произвольном сечении.

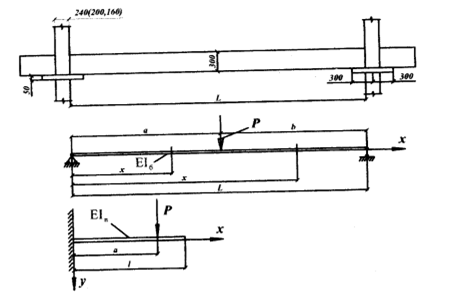
Рис. 1. Расчётная схема

Так как жесткость железобетонной балки многократно превышает жесткость опорной пластины, то деформируясь совместно, опорная пластина при определенных условиях будет повторять перемещения балки. При этом опорную стальную плиту можно рассматривать как некоторое упругое основание. Поскольку протяженность стальных опорных пластин на порядок меньше пролета балки, можно считать с некоторым приближением, что опорные пластины практически не влияют на характер деформирования балок.

Тогда, при условии, что стальная опорная пластина не теряет контакта с опирающейся на неё балкой, упругая линия балки запишется уравнением:

На участке а:

(1)

На участке b:

(2)

где: L - пролет балки (шаг колонн);

а - расстояние от опоры до точки приложения нагрузки;

Р - сосредоточенная нагрузка, приложенная к балке;

- изгибная жесткость балки.

В свою очередь, опорную стальную пластину можно рассматривать как консольную балку.

Уравнение упругой линии консольной пластины при нагружении сосредоточенной нагрузкой Р имеет вид:

(3)

где а - расстояние от точки приложения силы Р до начала координат;

- изгибная жесткость опорной пластины.

Решим уравнение (3) относительно Р:

(4)

Проложив у(х) = 1, получим выражение для коэффициента постели опорной пластины. В точке с координатой х, обозначая коэффициент постели через К, получим:

(5)

Тогда в случае расположения силы Р за пределами опорной пластины реактивный опор по линии контакта опорной пластины и балки опишется уравнением:

(6)

В случае, когда сосредоточенная сила расположена над опорной пластиной на расстоянии a от начала координат, реактивный опор на участке 0-а определяется по формуле (6), а правее точки приложения нагрузки Р по формуле:

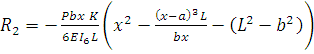(7)

Подставив в (6) и (7) значение К из (5), после преобразований получим соответственно:

(8)

и:

(9)

Значение реактивного отпора на конце опорной пластины

x = l = a = L-b

(10)

Эпюра контактных давлений имеет вид, приведенный на рис. 2.

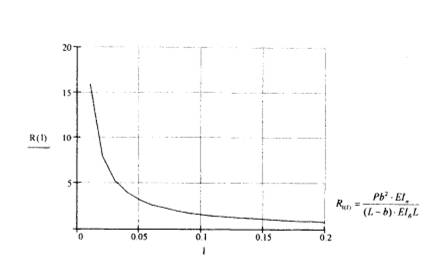
Рис. 2. Эпюра контактных давлений

Полученные выражения для контактных давлений (8, 9) справедливы, как оговаривалось выше, при полном контакте балки и опорной пластины. В случае если на части площади произойдет «отлипание» балки от опорной пластины, то задача определения контактных давлений будет являться существенно нелинейной и её решение требует специальных исследований.

Литература:

1. Мелихов С.В., Прокопенко В.С. Анализ методики определения эффективности разделения // Инновационные материалы, технологии и оборудование для строительства современных транспортных сооружений Белгородский государственный технологический университет им. В.Г. Шухова. 2013. С. 143-147.

2. Орехова Т.Н., Прокопенко В.С. Тонкодисперсные порошки для асфальтобетона // Научный альманах. 2016. № 1-1 (15). С. 465-467.

3. Прокопенко В.С., Шарапов Ринат Р., Агарков А.М., Шарапов Р.Р. Оптимизация работы оборудования для получения тонкодисперсных порошков // Вестник БГТУ им. В.Г. Шухова. 2015. № 1. С. 80-83.

4. Романович А.А. Особенности процесса постадийного измельчения материалов с использованием пресс-валкового агрегата// Известия высших учебных заведений. Строительство. 2007. № 9. С. 88-91.

5. Sharapov R.R., Prokopenko V.S. Modeling of the separation process in dynamic separators // World Applied Sciences Journal. 2013. Т. 25. № 3. С. 536-542.

6. Романович А.А., Орехова Т.Н., Мещеряков С.А., Прокопенко В.С. Технология получения минеральных добавок // Вестник БГТУ им. В.Г. Шухова. 2015. № 5. С. 188-192.

7. Прокопенко В.С., Решетов А.В. Совершенствование одноковшового экскаватора// В сборнике: Международная научно-техническая конференция молодых ученых БГТУ им. В.Г. Шухова БГТУ им. В.Г. Шухова. 2015. С. 846-849.