К.ф.-м.н.
Габасова О.Р.
Белорусский национальный технический
университет
О представлении
решения одной линейной гибридной системы управления
1. Пусть рассматривается
задача оптимального управления для гибридной [1] системы:
![]() ,
(1)
,
(1) 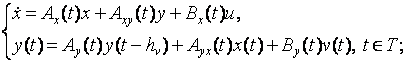 (2)
(2) ![]() (3)
(3) ![]() (4)
(4)
![]() . (5)
. (5)
Здесь ![]() ,
, ![]() – периоды квантования
времени,
– периоды квантования
времени, ![]() – заданные натуральные числа;
– заданные натуральные числа; ![]()
![]() ,
, ![]() ;
;![]()
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]() ,
, ![]()
![]()
![]() – кусочно-непрерывные функции;
– кусочно-непрерывные функции;![]() ,
,![]() ,
, ![]()
![]() , – непрерывные функции;
, – непрерывные функции; ![]() – состояние непрерывной части системы в момент времени
– состояние непрерывной части системы в момент времени ![]() ,
, ![]() – состояние дискретной части системы,
– состояние дискретной части системы, ![]() , – значения управляющих воздействий.
, – значения управляющих воздействий.
Пусть управляющие
воздействия ![]() , задачи (1) – (5) принадлежат классу дискретных функций
, задачи (1) – (5) принадлежат классу дискретных функций ![]()
![]()
![]() . Каждой паре управляющих воздействий (
. Каждой паре управляющих воздействий (![]() соответствует единственная траектория (
соответствует единственная траектория (![]() описываемая непрерывной функцией
описываемая непрерывной функцией ![]() и кусочно-непрерывной
функцией
и кусочно-непрерывной
функцией ![]() Пару
Пару ![]() назовем программой, если на ней выполняются (5)
и соответствующая ей траектория системы (2), (3) удовлетворяет ограничениям
(4). Программа
назовем программой, если на ней выполняются (5)
и соответствующая ей траектория системы (2), (3) удовлетворяет ограничениям
(4). Программа ![]() называется оптимальной,
если она доставляет критерию качества (1) максимальное значение.
называется оптимальной,
если она доставляет критерию качества (1) максимальное значение.
2. Формула Коши. Для исследования поставленной задачи важное значение как и в случае
обыкновенной линейной системы имеет формула Коши для решений. Пусть ![]() ,
, ![]() ,
, ![]() – управляющие воздействия,
– управляющие воздействия, ![]()
![]() , – соответствующая им траектория системы (2) с начальным условием
(3). В силу (2) имеет место тождество
, – соответствующая им траектория системы (2) с начальным условием
(3). В силу (2) имеет место тождество
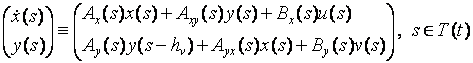 .
.
Умножим обе части тождества на пока
неопределенную матричную функцию
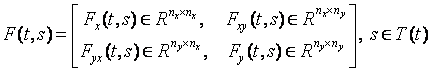 . (6)
. (6)
и проинтегрируем (6) в пределах от ![]() до
до ![]() :
:
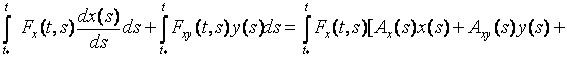
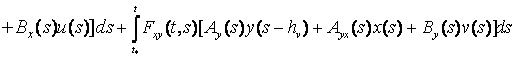 , (7)
, (7)
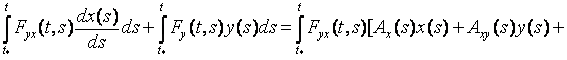
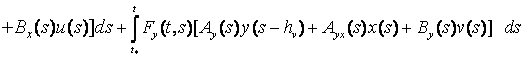 . (8)
. (8)
Пусть функции ![]()
![]()
![]() , дифференцируемыми по
, дифференцируемыми по ![]() . Преобразуем (7), (8):
. Преобразуем (7), (8):
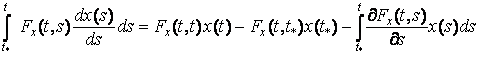 ;
(9)
;
(9)
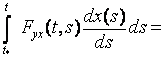
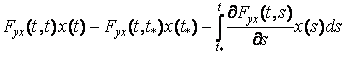 .
.
Т.к. ![]() ,
, ![]() ,
, ![]()
![]() то:
то:
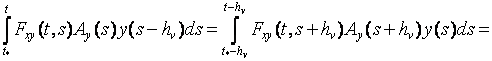
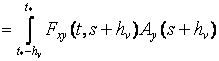
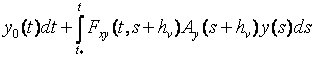 ; (10)
; (10)
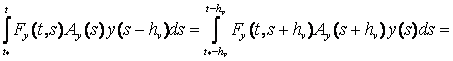
=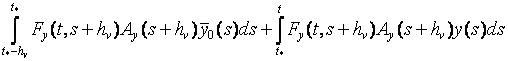 .
.
Используя (9), (10) для (7), (8) получим:

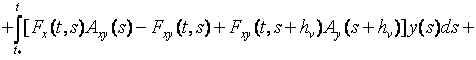 (11)
(11)
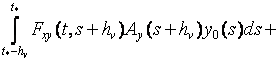
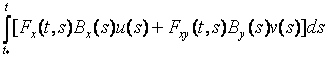 ;
;
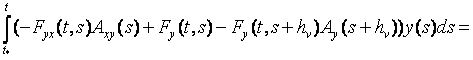
![]()
![]()
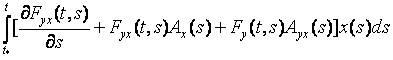 (12)
(12)
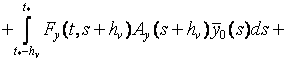
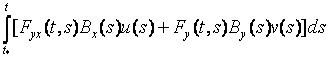 .
.
Пусть функция (5)
удовлетворяет соотношениям
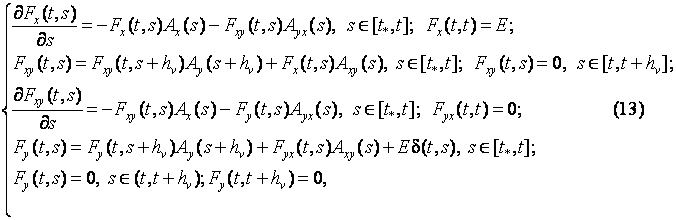
![]() (
(![]() если
если ![]() ).
).
Тогда соотношения (11), (12) примут
вид
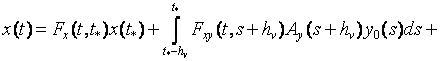
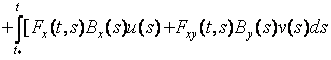 ,
,![]() (14)
(14) 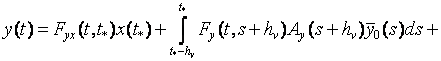
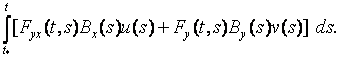
Формулы (13), (14) определяют решение
для уравнений (2) в задаче (1) – (5).
Можно получить другое, эквивалентное
представление для решений (2), которое более удобно для вычислений. Сделаем
замену независимой переменной ![]() и обозначим
и обозначим ![]() . Получим
. Получим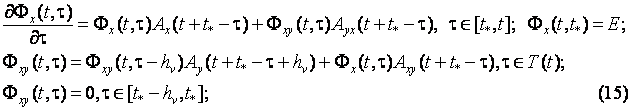
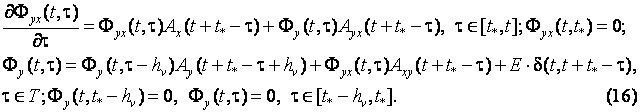 Из (16) видно,
что значения функции
Из (16) видно,
что значения функции ![]() , в точках
, в точках ![]() ,
, ![]() , содержит импульсную составляющую
, содержит импульсную составляющую ![]() . Матричная функция
. Матричная функция ![]() , удовлетворяет уравнению
, удовлетворяет уравнению
![]() (17)
(17)
Сужение функции ![]() на множество
на множество ![]() обозначим через
обозначим через ![]() . Тогда получаем
. Тогда получаем
![]() (18)
(18)
при ![]()
Функция ![]() , на промежутках непрерывности является решением уравнения
, на промежутках непрерывности является решением уравнения
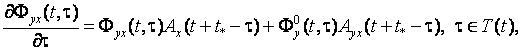 (19)
(19)
с начальным условием ![]() В точках
В точках ![]() она совершает скачки:
она совершает скачки:
![]() .
.
Следовательно, формула Коши (14) примет вид
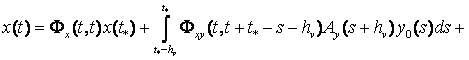
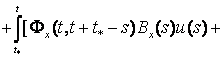
![]() ,
,
![]()
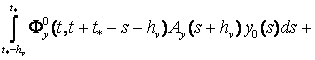
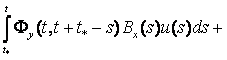
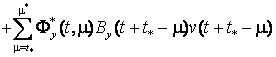
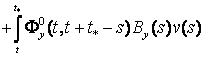
Опишем процедуру
вычисления функций (15) – (19). Учитывая тождество ![]() решаем однородное уравнение
решаем однородное уравнение ![]()
![]()
![]() , с начальным условием
, с начальным условием ![]() и находим
и находим ![]() ,
, ![]() . Затем, подставив найденную функцию
. Затем, подставив найденную функцию ![]() , во второе уравнение (15), вычисляем
, во второе уравнение (15), вычисляем ![]() ,
, ![]() . Повторив описанную процедуру на последующих промежутках, вычислим
. Повторив описанную процедуру на последующих промежутках, вычислим
![]() ,
, ![]() . Из (17) находим
. Из (17) находим ![]() . Поскольку
. Поскольку ![]() , то уравнение (19) на промежутке
, то уравнение (19) на промежутке ![]() становится однородным.
Решаем его с начальным условием
становится однородным.
Решаем его с начальным условием ![]()
![]() Из (19), находим
Из (19), находим ![]() ,
, ![]() . Из (18), построим
функцию
. Из (18), построим
функцию![]() ,
, ![]()
![]() , удовлетворяющую уравнению (19) с начальным условием
, удовлетворяющую уравнению (19) с начальным условием ![]()
![]() Продолжая процедуру, построим
Продолжая процедуру, построим ![]() ,
,![]() ,
, ![]() . На основе полученных формул для решения уравнений (2)
исследуется задача оптимального управления (1) – (5), сформулированная в п.1.
. На основе полученных формул для решения уравнений (2)
исследуется задача оптимального управления (1) – (5), сформулированная в п.1.
Литература
1.
Borelli F. Constrained optimal control of linear and hybrid systems // Lecture
Notes in Control and Information Sciences. – Springer, 2003. – Vol.290. – 293
p.
2. Габасова О.Р. Оптимизация линейных гибридных систем управления // Вестник БНТУ.
–2007. – № 2. – С. 71 – 75.