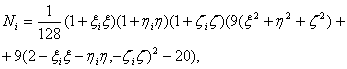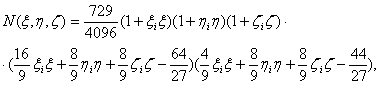Математика/Математическое моделирование
Козуб Н.А.
Херсонский национальный технический университет,
Украина
КОГНИТИВНАЯ КОМПЬЮТЕРНАЯ
ГРАФИКА В МОДЕЛИРОВАНИИ БАЗИСОВ СЕРЕНДИПОВЫХ
ЭЛЕМЕНТОВ
Введение
Одной
из главных функций человеческой жизнедеятельности есть познание, а новое
знание - основной результат этой познавательной активности человека. Когда
человек размышляет, в его сознании возникают воображаемые картины. Как правило,
условия прикладных задач задаются в виде текста, но в сознании человека любой
текст преобразуется в образ. Схема -
"интуиция, абстракция, символическая интерпретация" отражает процесс
познания математических объектов. Поэтому основная трудность при понимании
условия задачи заключается в том, чтобы представить условие в виде абстрактного
графического изображения. Сегодня о порождении нового
знания в голове человека можно говорить в контексте существенной зависимости от
современных информационных технологий. С этой точки зрения, виртуальная
реальность - это не только величайшее достижение современной информационной
индустрии, но и абсолютно новая технология решения любых проблем.
Существует
концепция так называемой когнитивной реальности, представляющей собой некую
интеллектуальную среду, погружаясь в которую, человек "общается" не с
виртуальными образами реальных (или "придуманных") объектов, а с
реальными, мультимедийными образами абстрактных (т.е. несуществующих в
"объективной реальности") объектов, понятий, и концепций данной
проблемной или предметной области. Цель такого общения человека с когнитивной
реальностью - жестко фиксирована: порождение нового знания. "Информатика - это наука о принципиально новой человеко-машинной
технологии расширенного
воспроизводства качественно нового знания" [1]. Базовым элементом
технологии когнитивной реальности является Когнитивная Компьютерная Графика.
Человеческое познание пользуется двумя механизмами
мышления. Один из них – возможность работать с абстрактными цепочками символов,
с которыми связаны некоторые семантические и прагматические представления. Это
– умение работать с текстами. Такое мышление можно назвать символическим или
алгебраическим. Другой – способность работать с чувственными образами и
представлениями об этих образах. Такие образы обладают большей конкретностью и
интегрированностью, чем символические представления. Но они значительно более
«расплывчаты», «менее логичны», чем то, что скрывается за элементами, с
которыми оперирует алгебраическое мышление. Но без них мы не могли бы отражать
в нашем сознании окружающий мир в той полноте, которая для нас характерна.
Способность работать с чувственными образами (и, прежде всего, со зрительными
образами) определяет то, что можно было бы назвать геометрическим мышлением
[2].
С помощью
компьютера можно увидеть еще не существующий объект, получить его
геометрические характеристики, выполнить исследование его физических свойств
путем постановки численных экспериментов, внести необходимые изменения,
подготовить производство и, наконец, изготовить объект. Инструментом для всего
этого служат CAD/CAM/CAE системы. Общим элементом таких систем является
математическая модель геометрии проектируемого объекта.
В работе с системами
геометрического моделирования используются различные области знания.
Теоретической основой геометрического моделирования являются дифференциальная и
аналитическая геометрии, вариационное исчисление, топология и разделы
вычислительной математики. Результатом геометрического моделирования объекта
является математическая модель его геометрии.
Используя геометрическую
модель, можно поставить численный эксперимент по определению
напряженно-деформированного состояния, устойчивости элементов конструкции,
тепловых, и других свойств объекта. Для этого дополняя геометрическую модель
физическими свойствами, моделируют внешние условия ее работы, выполняют
соответствующий расчет.
Анализ предшествующих публикаций, постановка задачи
Одной из перспективных
областей применения когнитивной графики является изучение плохо поддающихся
формализации моделей серендиповых конечных элементов (КЭ). Ранее, ввиду
отсутствия алгоритма построения моделей таких КЭ, их базисные функции, как
правило, определялись изобретательным подбором в виде неполных полиномов.
Этой проблемой занимались
с 1966-
Серендипова базисная
функция вдоль границ КЭ представляет собой полный полином и, следовательно,
имеет место непрерывность базиса при переходе межэлементной границы.
Проблема заключается в
создании альтернативных серендиповых моделей, обладающих перечисленными
свойствами и при этом не содержащих
кратных нулей, которые тоже нежелательны с вычислительной точки зрения [6]. Альтернативные
базисы создают возможность формулировать и решать прямые и обратные задачи о спектре
распределения по узлам равномерной массовой силы. Над альтернативными базисами
трикубических аппроксимаций КЭ работали Хомченко А.Н., Камаева Л.И., Гучек
П.И., Литвиненко Е.И., Манойленко Е.С [7,8].
Целью данной работы
является применение когнитивного компьютерного моделирования для
геометрического построения базисных функций серендиповых КЭ с акцентом на
особую роль классических поверхностей.
Основная часть
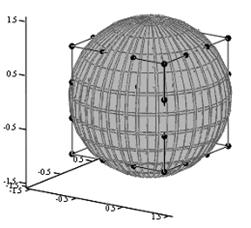
Рассмотрим трикубический 32
- узловой серендипов КЭ, изображенный на рис.1.
![]()
![]()
![]()
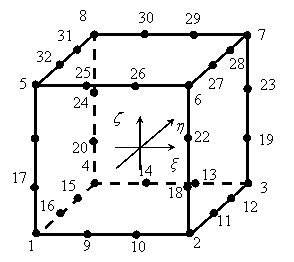
Рис.1 Трикубический КЭ серендипова семейства.
Узлы КЭ
расположены равномерно на ребрах куба, включая вершины. С каждым узлом
ассоциируется базисная функция, к которой предъявляются следующие требования:
1. Функция должна быть равна единице в
«своем» узле и нулю в остальных узлах, т.е.
![]() (1)
(1)
2. Сумма всех функций базиса должна быть
равна единице:
![]() (2)
(2)
Для стандартного КЭ и его модификаций
достаточно построить только две функции: в вершине и в промежуточном узле. В
таблице 1 представлены визуализации некоторых моделей. Как видно из таблицы,
для построения таких моделей трехмерного конечного элемента серендипова
семейства используются композиции плоскостей и поверхностей. Эти плоскости и
поверхности должны пересекать ребра КЭ в узлах, прилегающих к расчетному, что
гарантирует выполнение требования (1).
Таблица 1.
Визуализации моделей серендиповых конечных элементов
|
1.
«Модель со сферой». Базис: для угловых узлов
для узлов на сторонах
|
|
|
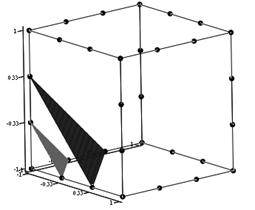
2. «Модель с треугольными пирамидами» Базис: для угловых узлов
для узлов на сторонах
|
|
|
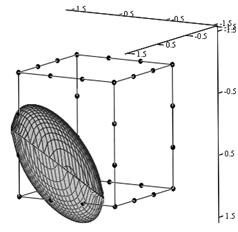
3. «Модель с эллипсоидом» Базис: для угловых узлов
для узлов на сторонах
|
|
|
4. «Модель с пересекающимися пирамидами» Базис: для угловых узлов
для узлов на сторонах
|
|
Таким образом, задача поиска новых
базисов серендиповых элементов может быть решена при помощи геометрического
моделирования и компьютерного эксперимента. Выполняя построение различных
плоскостей и поверхностей, проходящих через определенные узлы КЭ, исследуя их,
можно эффективно и наглядно получать различные базисы, в том числе и
неклассические (базисные функции серендиповых
интерполяций, в которых число параметров не соответствует числу узлов на
конечном элементе). Использование алгебраических методов для поиска таких
функций затруднительно, поскольку число неизвестных параметров системы
уравнений, описывающей значения этой функции в узлах не совпадает с
количеством уравнений.
Использование
же компьютерного моделирования в совокупности с когнитивной графикой позволяет
успешно справляться с такими задачами.
Выводы
Создание
альтернативных моделей трикубических
аппроксимаций КЭ с помощью когнитивной графики
позволяет решать актуальную задачу оптимизации базиса
и получать поверхности с заданными свойствами.
Синтез
когнитивной графики и вычислительного моделирования (когнитивное компьютерное
моделирование), позволяет, с одной стороны, существенно повысить познавательную
эффективность современных ЭВМ, а с другой - выявить и декодировать
целый класс артефактов, относящихся к категории когнитивных вычислительных
моделей.
Литература:
1.
Зенкин А.А. Когнитивная компьютерная графика/Под ред. Д.А.Поспелова — М: Наука,
1991. — 192 с.
2.
Зенкин А.А.,
Знание-порождающие технологии когнитивной реальности. - Новости Искусственного
Интеллекта, 1996, No. 2, стр. 72-78.
3.
Зенкевич
О. Метод конечных элементов в технике. – М.: Мир, 1975. – 541 с.
4.
Стренг
Г., Фикс Дж. Теория метода конечных элементов.- М.: Мир, 1977. – 349 с.
5.
Хомченко
А.Н. О базисных функциях МКЭ для уравнений в частных производных // III Респ. симпозиум по диффер. и интегр.
уравнениям: Тез. докл. – Одесса, 1982.- С. 257-258.
6.
Хомченко А.Н., Литвиненко Е.И., Гучек П.И. Геометрия серендиповых
аппроксимаций // Прикл. геом. и инж. графика. - К.: Будівельник, 1996. - Вып.
59. - С. 40-42.
7.
Гучек П.И., Литвиненко Е.И., Буба М.С., Хомченко А.Н.
Моделирование конечных элементов сирендипова семейства для исследования
температурных полей // Проблеми пожежної безпеки. - К.: МВС України. - 1995. -
С. 75-77.
8.
Манойленко О.С. Моделі скінчених елементів для розрахунків
температурних полів // Збірник наукових праць Херсонського філіалу Українського
державного морського технічного університету Випуск 1 - Херсон: ХФ УДМТУ. -
2003 .- С. 62-68.