Технические науки/2.Механика
К.т.н. Цепенюк М.И.
Тернопольский государственный
технический университет им. И.Пулюя
Оптимизация
параметров механизма подъема стрелы крана при динамических нагружениях
При работе крана подъем
груза осуществляется при помощи механизма подъема груза, а также с
использованием механизма подъема стрелы. Интенсификация современного
производства приводит к увеличению скоростей перемещения транспортируемых
грузов, что вызывает увеличение динамических нагрузок. Поэтому выбор таких параметров
подъемных механизмов, при которых в их элементах имеют место минимальные
динамические нагрузки, является актуальной задачей в процессе проектирования
грузоподъемных машин.
Цель настоящего
исследования – определение соотношения приведенной массы движущихся частей
механизма подъема стрелы и массы груза и соотношения жесткостей канатов подъема
стрелы и груза, при которых в канатах будут минимальные динамические нагрузки
при подъеме груза стрелой. Расчетную схему механизма подъема стрелы представим
в виде двухмассовой системы ![]() (рис. 1).
(рис. 1).
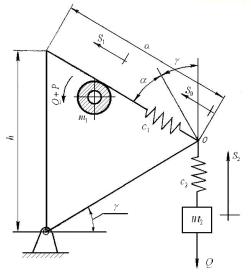
Рис. 1.
Здесь ![]() – приведенная масса
движущихся частей механизма подъема стрелы;
– приведенная масса
движущихся частей механизма подъема стрелы; ![]() – масса груза;
– масса груза; ![]() ,
, ![]() – жесткости канатов
подъема стрелы и груза; S
– жесткости канатов
подъема стрелы и груза; S![]() ,S
,S![]() , S
, S![]() – координаты
соответственно массы
– координаты
соответственно массы ![]() , конца стрелы (точки
, конца стрелы (точки ![]() ) и массы груза
) и массы груза ![]() ;
; ![]() – длина стрелы;
– длина стрелы; ![]() – высота мачты (стойки);
– высота мачты (стойки);
![]() – сила веса груза;
– сила веса груза; ![]() – приведенная
движущая (тормозная) сила, состоящая из силы
– приведенная
движущая (тормозная) сила, состоящая из силы ![]() , зависящей от
, зависящей от ![]() и угла
и угла ![]() , и из ускоряющей (замедляющей) силы
, и из ускоряющей (замедляющей) силы ![]() .
.
Составляя и решая
дифференциальные уравнения движения системы, можно без затруднений получить
(при некоторых допущений) формулы для определения максимальных динамических
нагрузок в канатах подъема стрелы и груза при подъеме груза стрелой ![]() :
:
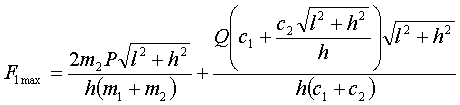 ; (1)
; (1)
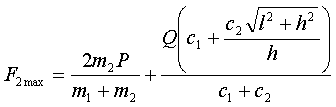 . (2)
. (2)
Примем обозначения
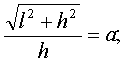
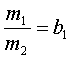 ;
; 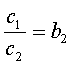 .
.
Тогда выражения (1), (2)
запишем в виде
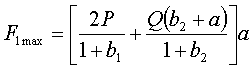 ;
; 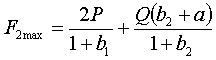 . (3), (4)
Сопоставляя зависимости (3) и (4), имеем
. (3), (4)
Сопоставляя зависимости (3) и (4), имеем
![]() . (5)
. (5)
В качестве переменных
проектирования примем величины ![]() ,
,![]() .
.
В связи с тем, что в
равенстве (5) коэффициент ![]() , величины
, величины ![]() ,
, ![]() будут иметь
экстремальные значения при одинаковых значениях переменных проектирования
будут иметь
экстремальные значения при одинаковых значениях переменных проектирования ![]() ,
,![]() . Поэтому функционал качества можно принять в виде
. Поэтому функционал качества можно принять в виде
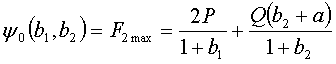 . (6)
. (6)
Пусть на значения
переменных проектирования наложены ограничения
![]() ;
; ![]() , (7)
, (7)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – положительные
числа.
– положительные
числа.
Выражения (7) запишем в
виде
![]() ;
; ![]() ; (8)
; (8)
![]() ;
; ![]() .
.
Таким образом, задача
оптимального проектирования приведена к минимизации функционала качества (6)
при четырех ограничениях в виде (8), наложенных на переменные проектирования.
Для решения задачи используем условия Куна-Такктера (2).
В нашем случае ![]() . Функции
. Функции ![]()
![]() , задающие ограничения, выпуклы, так как они линейны по
, задающие ограничения, выпуклы, так как они линейны по ![]() .
.
Используя (6), матрицу ![]() получим в виде
получим в виде
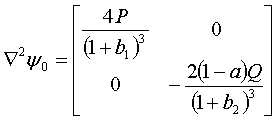 . (9)
. (9)
Матрица (9) положительно
определенная. Следовательно задача выпукла и если существует решение, удовлетворяющее
условиям Куна-Таккера, то оно будет оптимальным решением сформулированной
задачи нелинейного программирования.
Согласно условиям
Куна-Таккера, если точка ![]() является точкой
относительного минимума в задаче нелинейного программирования, то необходимо
чтобы существовал вектор
является точкой
относительного минимума в задаче нелинейного программирования, то необходимо
чтобы существовал вектор ![]() , такой, что
, такой, что
![]() ;
; ![]() ;
; ![]() ; (10)
; (10)
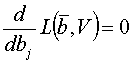 ;
; ![]() ,
,
где ![]() – лагранжиан.
– лагранжиан.
В нашем случае лагранжиан
имеет вид
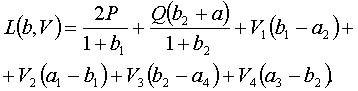 (11)
(11)
После подстановки
значений в выражения (10), имеем
![]() ;
; ![]() ;
;
![]() ;
; ![]() ; (12)
; (12)
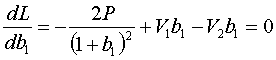 ;
;
 ;
;
Теперь необходимо решить
шесть уравнений (12) относительно неизвестных ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Трудность решения заключается в том, что согласно первым
четырем уравнениям из (12)
. Трудность решения заключается в том, что согласно первым
четырем уравнениям из (12) ![]() или
или ![]() . Поэтому необходимо рассмотреть шестнадцать вариантов
возможных значений
. Поэтому необходимо рассмотреть шестнадцать вариантов
возможных значений ![]() ,
, ![]() .
.
Исследовав все возможные
варианты, устанавливаем, что при ![]() ,
, ![]() удовлетворяются
условия (12) Куна-Таккера.
удовлетворяются
условия (12) Куна-Таккера.
Таким образом, если
переменные проектирования ![]() ,
,![]() примут наибольшие значения, то функционал качества
примут наибольшие значения, то функционал качества ![]() будет минимальным. По
отношению к рассматриваемой физической системе это значит, что если отношения
масс
будет минимальным. По
отношению к рассматриваемой физической системе это значит, что если отношения
масс ![]() и жесткостей
и жесткостей ![]() будут максимальными
из допустимых, то динамические нагрузки при подъеме груза стрелой в канатах
подъема стрелы и груза будут минимальными.
будут максимальными
из допустимых, то динамические нагрузки при подъеме груза стрелой в канатах
подъема стрелы и груза будут минимальными.
Отметим, что выбор
оптимальных параметров гидрокранов, расчетные схемы которых при исследовании
подъема груза стрелой могут быть представлены в виде двухмассовой системы,
можно произвести по аналогичной схеме.
Литература:
1.
М.С. Комаров. Динамика
грузоподъемных машин. – М.–К.: Машгиз, 1962, 268 с.
2.
Э. Хог, Я. Арора.
Прикладное оптимальное проектирование.–М.: Мир, 1983, 480 с.