Современные информационные технологии/ 4. Информационная безопасность

 

к.т.н. В.Г.Ткаченко, к.ф.-м.н. О.В.Синявский

Одесская национальная академия связи им. А.С.Попова, Украина

Построение корректирующего кода с использованием типов монотонных булевых функций

 

В процессе передачи информации по телекоммуникационным сетям связи возникает проблема исправления ошибок. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией. Одним из средств решения этих задач, является применение помехоустойчивых кодов, лежащих в основе систем кодирования-декодирования.

К настоящему времени разработано много различных помехоустойчивых кодов, отличающихся друг от друга основанием, расстоянием, избыточностью, структурой, функциональным назначением, энергетической эффективностью, корреляционными свойствами, алгоритмами кодирования и декодирования, формой частотного спектра ([1] … [4]). На основе максимальных типов [5] монотонных булевых функций (МБФ) построена криптосистема [6] с кодами, использующими деревья разложения типов МБФ.

Однако построенный код, используемый в [6], не предусматривает коррекцию ошибок.

Получены такие результаты.

ЛЕММА 1. Вектор  является кодовой последовательностью без ошибок тогда и только тогда, когда его правая (левая) максимальная часть и её дополнение являются максимальными типами.

ЛЕММА 2. Справедливо рекуррентное матричное уравнение:

                                 ,                                       (1)

где операция  - обычное умножение матриц.

Используя равенство, полученное в лемме 5 из [5]:

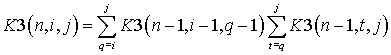               ,                     (2)

выведем матричную формулу, для построения матрицы Мn ранга типа n на основе матрицы  Мn-1  ранга типа .

Введём две операции. Операция «звёздочка слева» обозначает операцию добавления строки сверху и столбца слева таких: 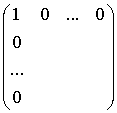, а операция «звёздочка справа» обозначает операцию добавления строки снизу и столбца справа. Обозначим через In – квадратную матрицу, порядка , которая получается из верхней треугольной матрицы порядка , состоящей из единиц, с помощью операции звёздочка слева. Обозначим через ** операцию транспонирования матрицы относительно побочной диагонали.

Обозначим через  верхнюю треугольную матрицу порядка  из единиц, тогда , а .

Следствие. Используя верхнюю треугольную матрицу из единиц  размерности , из (2) получим

                                .                                      (3)

ЛЕММА 3. Справедливо рекуррентное матричное уравнение:

                               .                                     (4)

Следствие 1. Для количества максимальных типов  справедливо выражение:

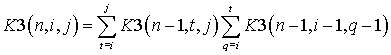               ,                     (5)

Следствие 2. Используя верхнюю треугольную матрицу из единиц  размерности , из (4), получим

                                .                                      (6)

Построение корректирующего кода. По определению все максимальные типы несравнимы, следовательно, если мы каждую компоненту максимального типа представим в виде двоичного числа заданной длины, то кодовое расстояние между любыми двумя типами не может быть меньше двух. Используя это свойство можно упростить построение кодов с минимальным кодовым расстоянием больше двух, за счёт сокращения базового множества двоичных последовательностей из которых эти коды строятся.

С ростом ранга количество типов МБФ сильно возрастает, поэтому используем не все, а только некоторые компоненты типа МБФ. Запишем каждую компоненту в двоичном виде и количество бит для каждой компоненты выберем  равное числу бит, с помощью которых можно записать максимальную компоненту среди всех компонент соответствующих этому номеру.

Для построения корректирующих кодов разработана программа, которая выводит максимальные типы определённого ранга для заданных границ, переводит их в двоичный код и вычисляет кодовое расстояние для этих кодов. В программе используются массив Т1, в котором содержатся максимальные типы ранга n – 1, и массив Т2, в котором содержатся максимальные типы ранга n. В обоих массивах типы упорядочены по возрастанию количества двоичных единиц, а типы с одинаковым количеством единиц упорядочены по возрастанию, как двоичные числа. Количества элементов массива Т2 с одинаковым количеством единиц представляет собой весовой спектр рассматриваемого кода. Имеются также дополнительные массивы Е1 и Е2, в которых содержатся индексы первых типов в массивах Т1 и Т2 с заданным количеством единиц. Максимальные типы обладают тем свойством, что типы с кодовым расстоянием 2 содержат одинаковое количество единиц. Таким образом, при нахождении типов с кодовым расстоянием не менее 3 необходимо просматривать только пары типов с одинаковым количеством единиц.

Кодирование происходит простым обращением к элементу массива Т2 с индексом равным блоку сообщения, т.е. элементы массива Т2 являются передаваемыми кодовыми словами. Рассмотрим алгоритм декодирования.

АЛГОРИТМ ДЕКОДИРОВАНИЯ:

Шаг 1. Находим в кодовом слове S количество k двоичных единиц.

Шаг 2. Выделяем из полученной последовательности максимальную правую часть S2 и её дополнение S1 (см. лемму 1). Этим уменьшается, по крайней мере, на порядок количество перебираемых типов [6]. Сдвиг-сумма . Находим количество единиц k1 в дополнении и k2 в максимальной правой части.

Шаг 3. Находим в массиве Т1 элементы с количеством единиц k2 с помощью массива Е1, т.е. индекс Е1(k2). Поиск слова S2 в массиве Е1 проводим методом деления пополам. Сначала находим индекс i1 среднего элемента массива Т1 с количеством единиц k2. Он равен целой части от Е1(k2) + (Е1(k2 + 1) – Е1(k2))/2. Если элемент Т1(i1) с индексом і1 равен S2, то устанавливаем флажок f2 и завершаем шаг 3. Если Т1(i1) больше S2, то копируем значение Е1(k2) в i2 и присваиваем i1 значение равное целой части от i2 + (i1 – i2)/2. Если Т1(i1) меньше S2, то копируем значение Е1(k2 + 1) в i2 и присваиваем i1 значение равное целой части от i1 + (i2 – i1)/2. Продолжаем аналогичные действия пока либо не найден элемент Т1(i1) = S2, либо не выполнится |i2 – i1| = 1. В первом случае флажок f2 будет установлен, а во втором нет.

Шаг 4. Находим в массиве Т1 элементы с количеством единиц k1 с помощью массива Е1, т.е. индекс Е1(k1). Если элемент Т1(i1) равен S1, то устанавливаем флажок f1. Поиск слова S1 в массиве Е1 проводим методом деления пополам как в шаге 3. Если элемент Т1(i1) с индексом і1 равен S1, то устанавливаем флажок f1, а если не найден, то не устанавливаем.

Шаг 5. Если флажки f1 и f2 установлены, то принятое кодовое слово представляется в виде сдвиг-суммы максимальных типов S1 и S2 ранга n – 1. Согласно лемме 1 в этом случае кодовое слово S принято без ошибок. В этом случае алгоритм заканчивается.

Шаг 6. Если флажок f1 или f2  не установлен, то находим в массиве Т2. элементы с количеством единиц k – 1 и k + 1 с помощью массива E2, т.е. индексы Е2(k – 1) и Е2(k + 1). Последовательно заменяем в кодовом слове S бит 0 на 1, а бит 1 на 0. После замены нуля на единицу ищем полученное слово S3 методом деления пополам начиная с индекса Е2(k + 1). После замены единицы на ноль ищем полученное слово S3 методом деления пополам начиная с индекса Е2(k – 1). При нахождении в массиве Т1 кодового слова S3 поиск прекращаем. В этом случае при передаче была одна ошибка и в действительности было передано кодовое слово S3, а не S2. Найденный индекс S3 равен блоку сообщений. Если в результате поиска кодовое слово S3 не найдено, то в принятом кодовом слове S имеется более одной ошибки.

 

Литература:

1.     Byers J. A Digital Fountain Approach to Reliable Sisttibuttion of Bulk Data. / J. Byers, M. Luby, M. Mitzenmacher, A. Rege // In SIGCOMM. - 1998.

2.     David J.C. Information Theory, Inference, and Learning Algorithms / J.C. David, MacKay - Cambridge University Press. - 2003.

3.     Luby M. LT Codes/ M. Luby // Of the 43rd Annual IEEE Symposium on Foundations of Computer Science (FOCS). - 2002. - Pp. 271-282.

4.     Варгаузин В.. Вблизи границы Шеннона / В. Варгаузин // ТелеМультиМедиа. - 2005. - №3. - C.3-10.

5.     Ткаченко В.Г. Перечисление типов монотонных булевых функций при синтезе цифровых схем / В.Г. Ткаченко // Наукові праці ОНАЗ ім. О.С. Попова. – 2008. – №2. – С. 54 – 69.

6.     Ткаченко В.Г. Деревья типов монотонных булевых функций и криптосистемы с блоками переменной длины / В.Г. Ткаченко, О.В. Синявский // Наукові праці ОНАЗ ім. О.С. Попова. – 2009. – №2. – С. 32 – 42.

7.     Ткаченко В.Г. Классификация монотонных булевых функций при синтезе цифровых схем / В.Г. Ткаченко // Наукові праці ОНАЗ ім. О.С. Попова. – 2008. – №1. – С. 35 – 43.