Математика/ 5. Математическое моделирование

К.ф.-м.н. Искакова А.С., Ибрагимов Б.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Моделирование наиболее подходящей несмещенной оценки распределения

При построении статистических оценок часто основным требованием является моделирование оценок с отсутствием систематических погрешностей в наблюдаемых данных. Иными словами, приоритетными статистическими оценками являются несмещенные. Как известно, для определенного распределения возможно смоделировать неединственную несмещенную оценку. То есть зачастую имеем множество несмещенных оценок, и желательно из представленных оценок выбрать ту, которая обладает приоритетными свойствами. Из хотя из практики, в таких случаях, выбирают оценку с наименьшим риском. Однако, встречаются ситуации, когда риски оценок являются эквивалентными или их построение является затруднительным. В представленной работе предложена обобщенная форма моделирования наиболее несмещенной оценки, обладающая хорошими асимптотическими свойствами.

Предположим, имеем множество несмещенных оценок

W(u)={W₁(u), …, W_μ(u)}

для вероятности распределения P(U=u). Рассмотрим задачу определения наиболее подходящей несмещенной оценки. Ранее в работах Искаковой А.С. приводился метод построения наиболее несмещенной оценки для одной модели распределения.

Определение. Несмещенная оценка W_g(u) для вероятности распределения P(U=u) является наиболее подходящей из всего множества несмещенных оценок оценок

W(u)={W₁(u), …, W_μ(u)},

если выполняется следующее соотношение

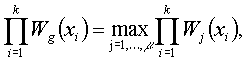(1)

где х=(x₁, ..., x_k) – реализация выборки объема k распределения P(U=u).

Следующая теорема является обобщением теоремы, приводимая в работах Искаковой А.С., и указывает на асимптотические свойства наиболее подходящих несмещенных оценок.

Теорема. Наиболее подходящая несмещенная оценка W_g(u) для распределения вероятности P(U=u) является состоятельной, асимптотически нормальной и асимптотически эффективной.

Лемма 1. Несмещенная оценка W(u) для распределения вероятности P(U=u) является п.н. функцией распределения вероятностей.

Доказательство леммы1. Из определения несмещенной оценки имеем, что

Е(W(u))=P(U=u).

Применяя свойство математического ожидания получим

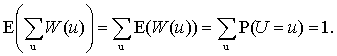
Таким образом, имеем корректность леммы.

Лемма 2. Оценки максимального правдоподобия для функции распределения W(u), представляемой несмещенной оценкой распределения вероятности P(U=u), являются состоятельными, асимптотически нормальными и асимптотически эффективными.

В силу асимптотических свойств оценок максимального правдоподобия имеем справедливость леммы 2.

Доказательство теоремы. Пусть для j=1,…, m

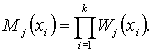
Из условия (1) следует, что

Очевидно, что при m®¥

z_g®q^*,

где q^*–вектор оценок максимального правдоподобия параметров распределения P(U=u). Значит, из леммы 2 следует, что наиболее подходящая несмещенная оценка W_g (u) для вероятности P(U=u) является состоятельной, асимптотически нормальной и асимптотически эффективной.

Таким образом, теорема является корректной.

Список используемой литературы

1. M. G. Kendall. "The advanced theory of statistics (vol. I). Distribution theory (2nd edition)". Charles Griffin & Company Limited, 1945.

2. M. G. Kendall and A. Stuart. "The advanced theory of statistics (vol. II). Inference and relationship (2nd edition)". Charles Griffin & Company Limited, 1967.

3. Papoulis А. Probability, random variables, and stochastic processes (3rd edition). McGrow-Hill Inc., 1991.

4. J. F. Kenney and E. S. Keeping. Mathematics of Statistics. Part I & II. D. Van Nostrand Company, Inc., 1961, 1959.

5. Blagouchine А. V. and E. Moreau: "Unbiased Adaptive Estimations of the Fourth-Order Cumulant for Real Random Zero-Mean Signal", IEEE Transactions on Signal Processing, vol. 57, no. 9, pp. 3330–3346, September 2009.

6. Ивченко Г.И., Медведев Ю.И. Математическая статистика. – М.: Высшая школа. 1984. – 248 с.

7. Крамер Г. Методы математической статистики. – М. 1975. – 648 c.

8. Искакова А.С. Об одном классе многомерных дискретных распределений вероятностей сумм прямоугольных матриц. // Известия МОН РК, НАН РК. 2001 г. № 5. С.85–89.

9. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.