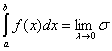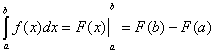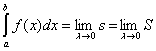Л.Н. Бадуленко, М.Р. Мухамедзянов

Лесосибирский педагогический институт – филиал ФГАОУ «Сибирский федеральный университет», Россия

О различных подходах к введению понятия определенного интеграла

Понятие интеграла (от лат. integer – целый) возникло в связи с потребностью, с одной стороны, отыскивать функции по их производным, а с другой – измерять площади, объёмы, длины дуг, работу сил за определённый промежуток времени и т.п. Соответственно с этим различают неопределенные и определённые интегралы, вычисление которых является задачей интегрального исчисления.

Интегральное исчисление – один из основных разделов математического анализа.

Существуют разные подходы к построению теории интегрального исчисления. Они отличаются неодинаковыми способами введения понятия определенного интеграла. В работе предлагаются три подхода: через интегральные суммы, через первообразные, через суммы Дарбу. Эти определения интеграла отражены в ниже приведенной таблице.

№	Название подхода	Определение определенного интеграла	Основные понятия
1	через интегральную сумму		интегральные суммы длинна дробления
2	через перво-образную F(x)		– непрерывная первообразная для ;
3	через суммы Дарбу	–нижняя сумма Дарбу; – верхняя сумма Дарбу;	– наименьшее и наибольшее значения функции на – м дроблении; – необходимое условие существования определенного интеграла.

_{Эквивалентность определений}

000Можно доказать, что все эти три определенные выше подхода к понятию определенного интеграла эквивалентны. Это означает следующее: если взять за определение определенного интеграла один подход, то два других будут выступать как свойства.

1. 0Докажем соответствие

Пусть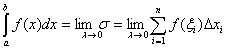

Если непрерывна на отрезке , и - некоторая первообразная функции , то 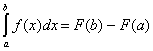. Функция 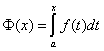- первообразная непрерывной функции. Так как - тоже первообразная, то . Положим в этом равенстве . Поскольку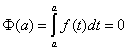, то 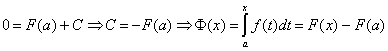. В равенстве 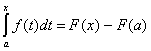пере обозначим переменные: для переменной интегрирования вернёмся к обозначению , верхний предел обозначим . Окончательно, .

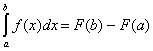Разность в правой части формулы обозначается специальным символом: (здесь читается как "подстановка от до "), поэтому формулу обычно записывают так: .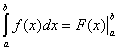

0_Дано

;

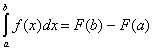Разобьём отрезок произвольным образом на частей точками

Домножим обе части равенства на и в качестве точки возьмём любую точку промежутка дробления .

затем суммируем по всем дроблениям

в предельном переходе получим

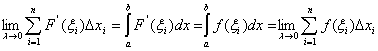
Тем самым мы показали, что первое определение эквивалентно второму.

0(1) (2)

2. Докажем соответствие

Разобьём отрезок произвольным образом на частей точками

Домножим обе части равенства на и в качестве точки xвозьмём любую точку промежутка дробления .

затем суммируем по всем дроблениям

в предельном переходе получим:

, а так как (по определению три)

0

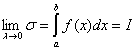- не зависит от способа дробления и выбора точек .

Разобьём отрезок произвольным образом на частей точками

Домножим обе части равенства на и в качестве точки возьмём любую точкупромежутка дробления .

Составим суммы и , где – наименьшее и наибольшее значения функции на – м дроблении. Тогда

Т.к. и являются частными случаями интегральной суммы, то

;;

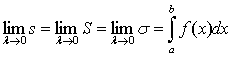Тем самым мы показали, что первое определение эквивалентно третьему.

(1) (3)251681792

3. Докажем соответствие

Воспользуемся свойством транзитивности эквивалентных функций

(1) (2) , (1) (3) => (2) (3)

Тем самым мы показали, что все три подхода к введению понятия определенного интеграла являются эквивалентными.

Эквивалентность различных подходов к понятию определенного интеграла позволяет рассматривать более широкий круг вопросов теории интегрального исчисления, использую при этом наиболее целесообразный подход.