Строительство и архитектура / 7. Водоснабжение и канализация
К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н.
Саратовский государственный технический университет
имени Гагарина Ю.А., Россия
Особенности кинематики потока со сдвигом перед цилиндром на твердом
основании
Часть 2*
Определение скорости нисходящих токов
В
каждой точке внутри кольца должно выполняться уравнение неразрывности (система
координат цилиндрическая).
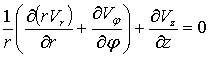 (1)
(1)
Далее,
имеем для составляющей ![]() :
:
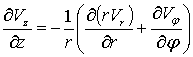 (2)
(2)
Подставляя
в (2) выражения для ![]() и
и ![]() , имеющие вид:
, имеющие вид:
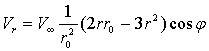 , (3)
, (3)
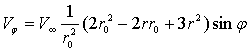 (4)
(4)
Получим:
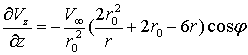 (5)
(5)
Для
определения ![]() , проинтегрируем (5) в
пределах от
, проинтегрируем (5) в
пределах от ![]() до
до ![]() , где
, где ![]() и
и ![]() – некоторые расстояния от дна.
– некоторые расстояния от дна.
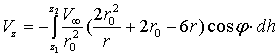 (6)
(6)
Интегрируя
(5) мы определяем ![]() , возможно, с точностью
до некоторой произвольной функции, не зависящей от
, возможно, с точностью
до некоторой произвольной функции, не зависящей от ![]() , которая обращается в ноль при дифференцировании по
, которая обращается в ноль при дифференцировании по ![]() .
.
Для
упрощения не рассматриваются поправки, связанные с этой произвольной функцией,
не зависящей от ![]() .
.
Заметим
также, что выбор пределов интегрирования, принятый в (6) не может быть
обоснован однозначно.
Для
определения ![]() возможно в (6) подставить любой закон
распределения скорости
возможно в (6) подставить любой закон
распределения скорости ![]() на бесконечности.
на бесконечности.
В
формуле (6) при ![]() величина
величина ![]() стремится
к бесконечности и, поскольку формула для
стремится
к бесконечности и, поскольку формула для ![]() приближенная,
то можно устранить эту особенность, приняв за
приближенная,
то можно устранить эту особенность, приняв за ![]() не ту скорость, которая имеет место в данном
горизонтальном слое в бесконечности, а скорость
не ту скорость, которая имеет место в данном
горизонтальном слое в бесконечности, а скорость ![]() по формуле (3); это тем более оправдано, что
по формуле (3); это тем более оправдано, что ![]() существует
только вблизи поверхности обтекаемого тела.
существует
только вблизи поверхности обтекаемого тела.
При
получении зависимости (6) необходимо следить за тем, чтобы при
дифференцировании ![]() формула (6) переходила в (5); этим условием
несколько ограничивается произвол при получении (6).
формула (6) переходила в (5); этим условием
несколько ограничивается произвол при получении (6).
Необходимо
заметить, что формула (3) действительна не при всех ![]() ; очевидно, что
; очевидно, что
![]() ,
,
тогда, должно быть
![]() ,
,
а следовательно, должно выполняться ограничение для ![]() :
:
![]() (7)
(7)
Для
случая ламинарного открытого потока распределение скоростей по глубине имеет
вид:
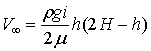 (8)
(8)
где ![]() – плотность жидкости;
– плотность жидкости;
![]() – ускорение
свободного падения;
– ускорение
свободного падения; ![]() – геометрический
уклон;
– геометрический
уклон; ![]() – динамический
коэффициент вязкости;
– динамический
коэффициент вязкости; ![]() – глубина потока;
– глубина потока; ![]() – расстояние от дна
до слоя, скорость которого равна
– расстояние от дна
до слоя, скорость которого равна ![]() .
.
Для
турбулентного открытого потока можно принять степенной закон распределения
осредненных скоростей по глубине в виде:
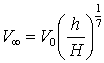 , (9)
, (9)
где ![]() – расстояние от дна по вертикали до рассматриваемого сечения,
– расстояние от дна по вертикали до рассматриваемого сечения,
![]() – скорость на
поверхности.
– скорость на
поверхности.
Преобразовав
выражение (8) с целью явного выделения скорости жидкости на свободной
поверхности:
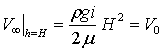 (10)
(10)
тогда:
![]() (11)
(11)
С учетом
сделанных ранее замечаний, возможно получить несколько различный выражений для ![]() (при ламинарном
режиме), выбирая различные пределы интегрирования:
(при ламинарном
режиме), выбирая различные пределы интегрирования:
Ι. 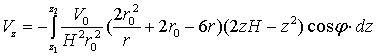 (12)
(12)
или:
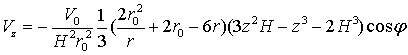 (13)
(13)
В (13)
пределы интегрирования взяты так, чтобы перед ![]() оказывался знак «-»; зависимость (12) взяты из уравнения
неразрывности без изменений; основной недостаток ее – стремление
оказывался знак «-»; зависимость (12) взяты из уравнения
неразрывности без изменений; основной недостаток ее – стремление ![]() к бесконечности
к бесконечности ![]()
ΙΙ. 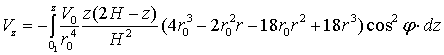 (14)
(14)
или:
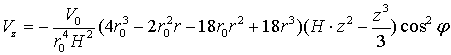 (15)
(15)
В
данном случае вместо ![]() взято выражение для
взято выражение для ![]() и тем самым стало при
и тем самым стало при
![]() ,
, ![]() ; кроме того, взяты другие пределы интегрирования.
; кроме того, взяты другие пределы интегрирования.
ΙΙΙ. 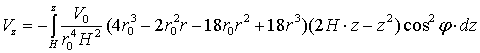 (16)
(16)
или:
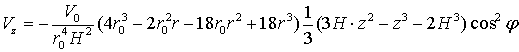 (17)
(17)
В
данном случае, по сравнению с предыдущими, взяты другие пределы интегрирования.
ΙV. 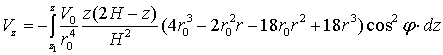 (18)
(18)
или:
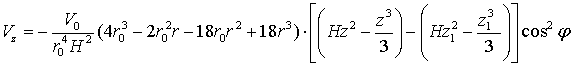 (19)
(19)
В
последнем варианте взяты пределы интегрирования по глубине от ![]() до
до ![]() и, таким образом,
можно рассмотреть полосу в вертикальной плоскости любой протяженности, но
величина интеграла (величина
и, таким образом,
можно рассмотреть полосу в вертикальной плоскости любой протяженности, но
величина интеграла (величина ![]() ) будет зависеть от ширины этой полосы (
) будет зависеть от ширины этой полосы (![]() ).
).
Основной
недостаток зависимостей для ![]() ,
, ![]() и
и ![]() состоит в том, что
при их выводе было использовано только уравнение неразрывности, но не были
использованы уравнения движения.
состоит в том, что
при их выводе было использовано только уравнение неразрывности, но не были
использованы уравнения движения.
(*) 1-я часть была опубликована в материалах
конференции «Образование и наука без границ», Польша, 07-15 декабря 2012.