Айткулов А.У., Ажиханов Н.Т., Курманбеков Р.С., Мугалбекова А.А.

Каспийский государственный университет технологий и инжиниринга

имени Ш.Есенова (г.Актау, Казахстан)

 

                                                    

МОДЕЛЬ ДЛЯ ОЦЕНКИ ИЗМЕНЕНИЯ ДЕБИТА СКВАЖИНЫ С ВЕРТИКАЛЬНОЙ ТРЕЩИНЫ В ПЛАСТЕ

 

         Практика  разработки нефтяных и газовых месторождений показывает, что  при проведении гидроразрыва пласта (ГРП) в призабойной зоне пласта (ПЗП)  скважины в первую очередь образуется трещины по вертикальной плоскости, т.е. вертикальные трещины. Для принятия решения по проведению мероприятий ГРП [1], на предмет стоит ли проводит такую работу, для увеличения производительности пласта-коллектора в ПЗП, необходимо выполнить оценочные технологические расчеты. В связи с этим данная работа посвящена исследованию по оценке технологической эффективности вертикальной трещины при проведении ГРП. Для выполнения работы рассматривается круговой пласт с радиусом контура питания Rk.

            Если радиус контура питания Rк ≥ Rо, то контур питания и трещину без большой погрешности можно принять за два конфокальных эллипса.

Если принять К2=∞, т.е. считать что давление в трещине Ртр=Рс, то для определения qн и qв (соответственно низкие и высокие значения дебитов скважин) можно воспользоваться решением, приведенным в работе          И.А. Чарного [2]

         Если предположить, что приток жидкости происходит не только к трещине (принятой за эллипс), но, а также влияние самой скважины на приток будет учитываться явлением притока через не нарушение пласта, то такой приток будет значительно больше притока к скважине и  трещине, т.е. будет больше дебита скважины.

         Согласно решению, приведенному в работе [2] с учетом результатов работы [4], приток к трещине (эллипсу) определяется по формуле:

;                                        (1)

Определение минимального прироста дебита скважины осуществляется следующим путем.

         Приток к эллипсу, в который полностью вписаны скважина и трещина  будет меньше притока только к скважине и трещине, если принять давление на контуре эллипса Р=Рс´ причем Рс´>Рс.. Если использовать это предположение, то таким эллипсом могут быть эллипс с полуосями  и . Тогда величина притока, т.е. дебита жидкости к этому эллипсу, согласно работам [2 и 3].

         Относительной увеличение qн по сравнению с qс будет определяться по следующей формуле

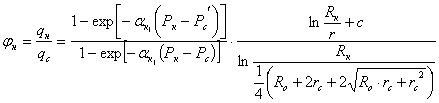                (2)

         Таким образом, по полученным формулам (1) и (2) можно определить границы, между которыми находится действительная величина дебита при наличии в пласте вертикальной трещины.

Для примера используем следующие данные:

а)  радиус контура питания             Rк = 1000 м.

б)  радиус скважины                       rc  = 0,1 м.

в)  коэффициент несовершенства скважины, как по степени,

     так и по характеру                      с = 2,1

г)  толщина пласта                          h1 = 10 м.

д)  проницаемость пласта               К1.0 = 0,25 дарси = 0,25·10-12 м2.

е)  проницаемость трещины           К2 = 83300 · δ2.

ж)  радиус трещины                        Ro = 25 м.

з)  величина раскрытия трещины  δ = 1 мм..

и)  давление на контуре питания    Рк = Ро = 25 МПа..

к)  давление на забое скважины     Рс = 18 МПа..

л)  коэффициент изменения гидропроводности пласта .

м)  величина давления                    Рс´ = 21 МПа.

         Результаты расчетов свидетельствуют о том, что прирост дебита скважины при образовании вертикальной трещины в основном зависит от изменения размеров трещин и гидродинамических параметров образованных вертикальных каналов.

 

                                     Зависимость φв и  φн  от  Ro  при  К1 = 0,25 мкм2.

в условиях образования вертикальной трещины

 

 

 


φв
 
                                                             φ               6

 

φср
 
                                                               4

φн
 
 

 


                                                               2

 

 

                                                               0                  25            50             75          100  Ro,м

 

Рисунок 1.

 

         График зависимости изменения параметра φ от  Ro при образовании вертикальной трещины, построенный при различных значениях Ro´ приведены на рисунке 1.

 

                                                   ВЫВОДЫ

         1. Из построенных графиков зависимости φ  и  Ro видно, что верхние и нижние пределы увеличения дебита скважины при образовании горизонтальной и вертикальной трещин из-за гидравлического разрыва в призабойной зоне пласта имеют значительные расхождения между собой. Это, по-видимому, связано с влиянием на процесс гидроразрыва, пластичности пласта и упругости жидкости, которые значительно влияют при формировании трещины.

         2. Из результатов анализа расчетных данных следует, что чем меньше ширина трещины, тем соответственно и снижается эффективность гидравлического разрыва пласта, образованного в горизонтальной плоскости, а также с увеличением параметра Ro уменьшается темп роста коэффициента φ.

 

 

 

                                              Литература

 

1.      Малышев А.Г., Малышев Г.А., Журба В.Н., Сальникова Н.Н. Анализ технологии проведения ГРП на месторождениях ОАО «Сургутнефтегаз». «Нефтяное хозяйство». 1997. №9. С. 46-51.

2.      Щелкачев В.Н. Основы приложения и теория неустановившейся фильтрации.  М.: Нефть и газ, 1995. – Ч. 1.- 586 с., Ч. 2.- 493 с.

3.      Басниев К.С. Дмитриев Н.М., Каневская Р.Д., Максимов В.М. Подземная гидромеханика.-М.-Ижевск:Институт компьютерных исследований, 2006.-488 с.

4.      Горбунов А.Т.  Разработка аномальных нефтяных месторождений. М.,

     Недра, 1981, 237 с.