Ищенко А. А., Ширяев А.В., Ширяев И.А.
КОНТАКТНЫЕ НАПРЯЖЕНИЯ УПРУГИХ ТЕЛ ПРИ ДЕЙСТВИИ СИЛ
ТРЕНИЯ НА ПЛОЩАДКЕ КОНТАКТА
Впервые задача о вдавливании в упругое полупространство штампа
с плоским основанием произвольной формы в плане рассмотрена Л. А. Галиным [1].
Им получены значения верхней и нижней оценок для величины силы, под действием
которой штамп перемещается поступательно на заданную глубину. Задача о давлении
на упругое полупространство квадратного в плане штампа исследовалась в работах
М. Я. Леонова, С. А. Посацкого, А. Н. Иващенко, В. М. Леоновой [2]. Несмотря на достаточное количество работ, посвященных
контакту тел различной формы не существует достаточно простого решения для
контакта двух упругих тел.
 В
данном случае рассмотрены два вида плоской задачи теории упругости. Считаем, что длина тел значительно больше их
размеров по оси х, поэтому задача
сводится к плоской деформации (перемещение точек тел вдоль площадки контакта
отсутствует, но напряжения вдоль площадки не равны нулю). На каждое сечение
действует удельная сила Р, равная
отношению суммарной нагрузки к длине тел.
В
данном случае рассмотрены два вида плоской задачи теории упругости. Считаем, что длина тел значительно больше их
размеров по оси х, поэтому задача
сводится к плоской деформации (перемещение точек тел вдоль площадки контакта
отсутствует, но напряжения вдоль площадки не равны нулю). На каждое сечение
действует удельная сила Р, равная
отношению суммарной нагрузки к длине тел.
Решение этой задачи
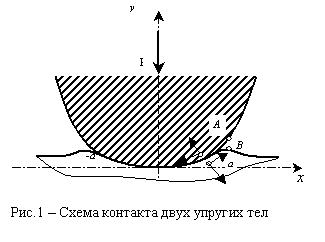
выполняется по методике [1]. Полагаем, что радиусы кривизны обоих тел велики по сравнению с размерами площадки контакта и
поэтому, каждое из этих тел можно заменить полуплоскостью (рис. 1). Начало
координат поместим в точке первоначального касания тел. Рассмотрим два
варианта данной задачи: контакт в условиях отсутствия сил трения и при наличии
сил трения, если одно из тел имеет
микро - или макроперемещения (что характерно для контакта деталей
металлургических машин).
Тогда граничные
условия выглядят следующим образом:
1. Случай, когда
на площадке контакта отсутствуют силы трения. Тангенциальные
усилия отсутствуют.
2. Случай, когда на площадке
контакта имеют место силы трения. Пусть коэффициент трения равен ρ.

Используя алгоритм решения, приведенный в работе [1] и
опуская промежуточные выводы, получим следующее
решение. Изменение контактных напряжений в интервале, где -a
< х < a
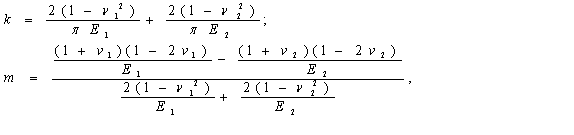
где
Е1 и Е2 – модули продольной
упругости контактирующих тел, а ν1 и ν2 – коэффициенты Пуассона.
![]()
В отличие от работы [1], показатель θ учитывает упругие свойства обеих
контактирующих тел:
Для
удобства исследования распределения нормального давления на площадке контакта
введем

безразмерную
координату ξ=x/a (-1 < ξ < +1), тогда:
Вышеприведенное решение задачи при наличии сил трения
является более общим случаем. Его можно легко применить и для случая отсутствия
сил трения, т.е. в этом случае ρ=0.
Тогда показатель θ=½ и, подставляя его значение в (2) получим формулу
давления на поверхности упругого тела
без трения в контакте. Это выражение идентично зависимости, полученной для
контакта абсолютно жесткого штампа с упругой полуплоскостью.
Особенностями зависимостей (1) и (3) является то, что
показатель степени (1/2 – θ)
должен быть положительным. То есть, в формулах коэффициентов k и m первое тело – всегда обладает
более упругими свойствами, в противном случае сила трения меняет направление и
знак степени в этих формулах следует изменить на обратный. Кроме того, вышеприведенные зависимости
неприменимы для случая контакта двух тел, с равными упругими характеристиками.
Тогда показатель θ обращается в
ноль и давления в выражениях (1), (3) тоже равны нулю, чего не может быть.
![]()
 В
качестве примера рассчитаны контактные напряжения для тел из эпоксидной смолы
(Е1=3·104 кг/см2, ν1=0,35) и
стали (Е2=2,1·106 кг/см2, ν2=0,3).
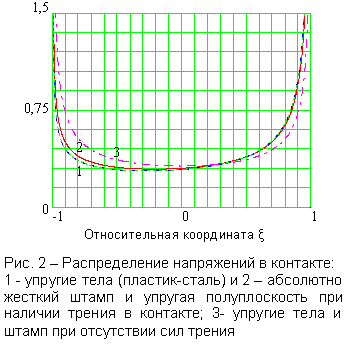
Графики изменения относительных давлений вдоль площадки контакта в
относительных координатах для двух рассмотренных случаев, представлены на рис.
2. Очевидно, что при таком соотношении упругих характеристик распределение
давления в контакте сталь-материал на основе эпоксидной смолы весьма близки к
давлению штампа с упругой полуплоскостью.
В
качестве примера рассчитаны контактные напряжения для тел из эпоксидной смолы
(Е1=3·104 кг/см2, ν1=0,35) и
стали (Е2=2,1·106 кг/см2, ν2=0,3).
Графики изменения относительных давлений вдоль площадки контакта в
относительных координатах для двух рассмотренных случаев, представлены на рис.
2. Очевидно, что при таком соотношении упругих характеристик распределение
давления в контакте сталь-материал на основе эпоксидной смолы весьма близки к
давлению штампа с упругой полуплоскостью.
Выводы
1. Выведены теоретические зависимости
контактных напряжений двух упругих тел, одно из которых имеет конечные размеры как
для случая наличия сил трения в контакте, так и в случае их отсутствия.
2. Выявлено ограничение в применении
полученных зависимостей для тел с близкими упругими свойствами.
Список
использованных источников:
1. Галин Л. А. Контактные задачи теории упругости.—М. : Гостехиздат,
1953.— 264 с.
2. Развитие теории контактных задач в СССР / Под общ. ред.
Л. А. Галина и др.— М. : Наука, 1976.— 492 с.