Исследование вращающего момента на заторможенном валу

импульсного механизма инерционной передачи

Инерционные бесступенчатые передачи являются передачами механического типа и позволяют автоматически и бесступенчато менять режимы работы в зависимости от нагрузки [1]. Принцип работы инерционных передач основан на использовании знакопеременного момента, генерируемого импульсным механизмом.

Одной из основных характеристик импульсного механизма, позволяющей оценить возможность его применения в приводе той или иной машины, является среднее значение вращающего момента от инерционных сил грузовых звеньев на заторможенном промежуточном валу, действующего в течение положительной части цикла. Найдем аналитическое выражение для среднего значения этого момента.

Для обобщенной схемы импульсного механизма система дифференциальных уравнений движения, полученная с помощью уравнений Лагранжа, имеет вид [2]:

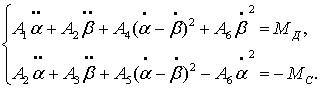(1)

Во втором уравнении системы (1) положим . Это допущение широко используется в различных теоретических работах по исследованию инерционных передач [3]. Рассматривая теперь наиболее нагруженный режим работы импульсного механизма ─ режим заторможенного промежуточного вала (), получаем

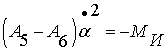, (2)

где

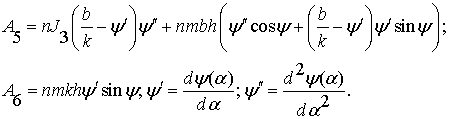
Пусть . Тогда обе части уравнения (2) можно разделить на переменную :

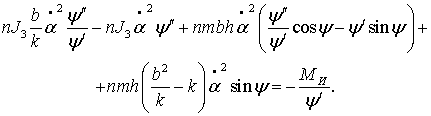(3)

Проведем почленное интегрирование уравнения (3):

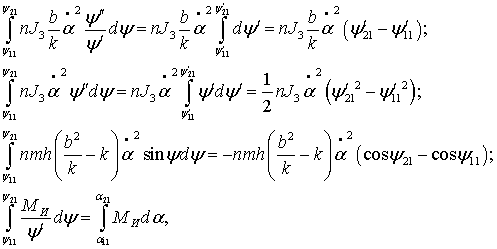
где ─ пределы интегрирования.

Используя теорему о среднем значении интеграла в предположении непрерывности функции , находим

.

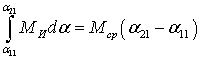Здесь ─ среднее значение момента от инерционных сил грузовых звеньев, действующего на заторможенный промежуточный вал на отрезке

Третье слагаемое уравнения (3) представляет собой производную по углу от выражения , поэтому

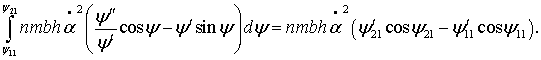
По результатам почленного интегрирования уравнения (3) найдем аналитическое выражение для среднего значения момента, действующего на заторможенный ведомый вал импульсного механизма в течение положительной части цикла:

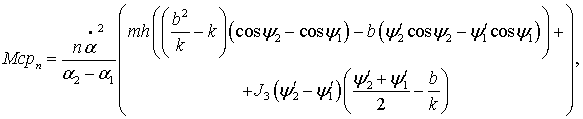(4)

в котором ─ значения переменных в начале и конце действия положительного импульса.

Нетрудно показать, что зависимость (4) включает в себя известное выражение для импульсных механизмов гармонического семейства () [1]. Действительно, для этих механизмов Тогда из соотношения находим: Подставляя полученные значения в выражение (4), найдем:

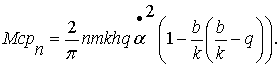
Уже на первом этапе анализа выражения (4) можно сделать некоторые выводы. Так, полагая , получаем:

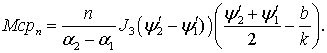(5)

Для импульсных механизмов негармонического семейства в общем случае Следовательно, такие механизмы и при уравновешенных грузовых звеньях осуществляют трансформацию вращающего момента в конструкциях инерционных передач. Это обстоятельство находит физическое объяснение. При равномерном вращении ведущего маховика и заторможенном ведомом валу импульсного механизма грузовые звенья импульсного механизма негармонического семейства совершают неравномерное вращение в относительном движении. Вследствие неравномерности вращения грузовых звеньев возникают тангенциальные силы инерции, которые и создают знакопеременный момент на ведомом валу импульсного механизма. Таким образом, способность импульсных механизмов негармонического семейства с уравновешенными грузовыми звеньями осуществлять трансформацию момента обусловлена действием тангенциальных сил инерции. Среднее значение момента за положительную часть цикла при этом определиться по выражению (5).

Проведем, например, расчет среднего значения момента, действующего на заторможенный ведомый вал непараллелограммного импульсного механизма в течение положительной части цикла.

Для рассматриваемого импульсного механизма угол поворота и производная определяются по выражениям [4]:

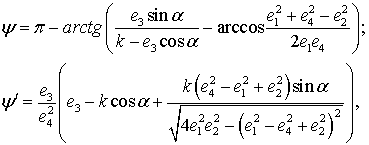
где

Производную найдем, продифференцировав функцию по углу поворота

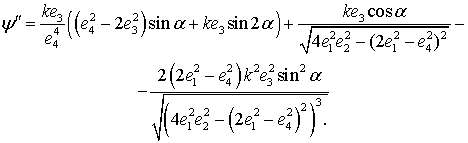
На рис.1 показаны графики зависимостей от угла поворота ведущего звена для непараллелограммного импульсного механизма, имеющего следующие параметры:

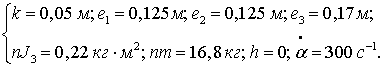(6)

Результаты расчета момента для этого механизма по выражению (2) приведены на рис.2. Как видно из рис.2, положительная часть цикла складывается из двух импульсов. Среднее значение момента за положительную часть цикла , подсчитанное по формуле (5), составляет 1411 Нм.

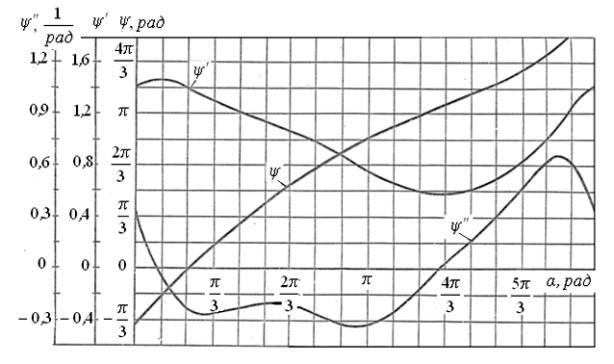
Рис.1. Графики зависимостей от угла поворота

Для сравнения проведем расчет среднего момента для непараллелограммного импульсного механизма, имеющего те же самые параметры (6), за исключением лишь того, что грузовые звенья выполнены неуравновешенными ().

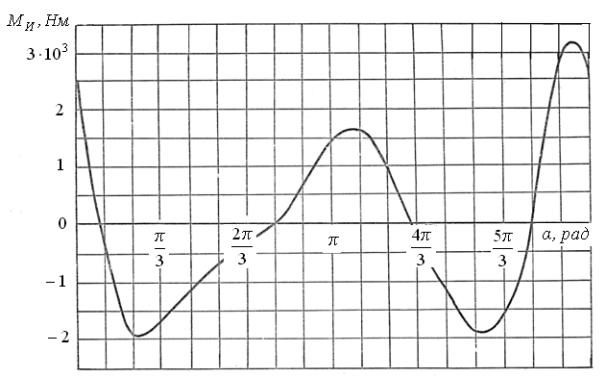
Рис.2. График зависимости момента, действующего на заторможенный промежуточный вал, от угла поворота

Выражение (2) представим в виде суммы ,

где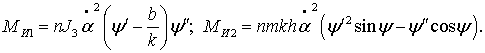

Графики представлены на рис.3. Среднее значение момента, подсчитанное по формуле (4), составляет 3766 Нм.

Анализ полученных результатов показывает, что тангенциальные силы инерции оказывают меньшее влияние на среднюю величину вращающего момента по сравнению с действием центробежных сил инерции. Увеличение среднего момента за счет тангенциальных сил инерции нецелесообразно. Действительно, как следует из выражения (5), момент можно повысить, увеличив разность , т.е. увеличив неравномерность вращения грузовых звеньев, но повышение неравномерности вращения грузовых звеньев отрицательно сказывается на нагрузках, действующих на импульсный механизм, и приводит к неравномерности вращения ведущего маховика [3].

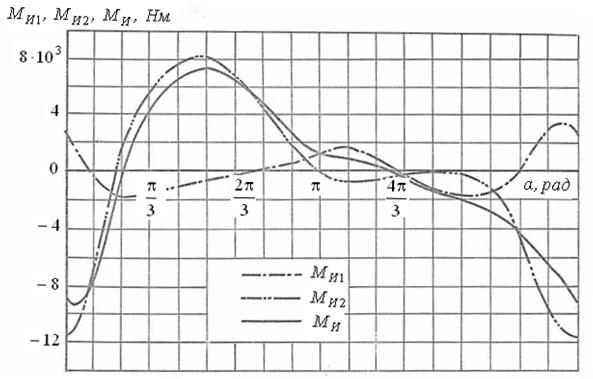
Рис.3. Графики зависимостей моментов от угла поворота

Увеличение момента на основе тангенциальных сил инерции может быть достигнуто и за счет повышения момента инерции грузовых звеньев , что приводит к возрастанию неравномерности вращения ведущего маховика, а, следовательно, и к неравномерности вращения двигателя.

Литература:

1. Леонов А.И. Инерционные автоматические трансформаторы вращающего момента. М.: Машиностроение, 1978. 224 с.

2. Алюков С.В. Совершенствование математических моделей инерционных трансформаторов вращающего момента // Вестник машиностроения, Москва, 2010, №7, C. 3─10.

3. Алюков С.В. Динамика инерционного трансформатора вращающего момента без механизмов свободного хода: Автореф. дис. …канд. техн. наук, ВПИ, 1983.

4. Артоболевский И. И. Теория механизмов и машин: Учеб. для втузов. — 4-е изд., перераб. и доп. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — 640 с.