Химия и химические технологии/5.

Фундаментальные проблемы создания новых материалов и технологий.

 

К.т.н.  Налетов В.А., д.т.н. Глебов М.Б., д.т.н. Налетов А.Ю.

 

Российский химико-технологический университет им. Д.И. Менделеева,

г. Москва, Российская Федерация, E-mail: energo@muctr.ru,

Оптимальная организация химико-технологической системы на основе декомпозиции задачи по иерархическим уровням. Информационный подход

 

При автоматизированном проектировании химических производств наиболее сложной проблемой является процедура синтеза химико-технологических систем (ХТС) с неоднородной структурой. Принципиально иной подход и иную стратегию выбора оптимального решения можно предложить на основе информационной концепции, основанной на критерии организованности ХТС.

Рассмотрим подход к синтезу такой системы с позиции информационно-термодинамического подхода на основе декомпозиции задачи по иерархическим уровням.

В работе [1] для описания химико-технологической системы с позиции теории информации был введен многоуровневый критерий ее организованности, характеризующий общую тенденцию систем к повышению показателей их целостности, макроскопичности и автономности. Было показано, что в организации ХТС доминирующую роль играют показатели макроуровня в виде весовых коэффициентов, оптимальный выбор которых характеризует объективно наилучший вариант согласования процессов в системе в соответствии с нулевым законом термодинамики.

В соответствии с эволюционным законом усложнения или системной организации организмов, а также всех технических, биологических и социальных систем (закон К.Ф. Рулье) любая система стремится оптимальным образом дифференцировать свои функции между элементами для обеспечения высокой степени организованности системы в целом.

Таким образом, эволюционный синтез химико-технологической системы подразумевает процесс ее усложнения, при котором количество элементов в ней возрастает до уровня, необходимого для реализации цели преобразований. Для оценки процесса усложнения ХТС в работе [2] предложены критерии пошагового усложнения или эволюционного синтеза. Общей составляющей критерия любого уровня усложнения ХТС является безразмерная стоимость единицы информации в виде:

 ,                                                                 (1)

 где n – весовой коэффициент в виде вероятности флуктуации среднего термодинамического уровня преобразования, K – безразмерный фактор затрат на организацию процесса, ηT – термодинамический КПД процесса.

Выбор оптимального решения определяется минимизацией критерия вида (1) по аналогии с минимизацией стоимости единицы эксергии в эксергоэкономическом подходе [3].

Однако при большом количестве элементов в ХТС вид критерия существенно усложняется, что затрудняет вычислительные процедуры поиска оптимального решения. Поэтому в данной работе предлагается на основе приоритетов характеристик макро- и микроуровней в повышении организованности ХТС осуществлять декомпозицию задачи поиска оптимального решения.

Стратегию выбора оптимального решения будем осуществлять по схеме «сверху-вниз» от системы к процессу в двухуровневом алгоритме:

-  во-первых, определение оптимальных весовых коэффициентов или вкладов процессов, исходя из оптимальных условий организации макроуровня ХТС;

- во-вторых, поиск для определенных на верхнем уровне весовых коэффициентов оптимальных условий проведения целевого превращения вещества или подстройка целевого превращения под данные прогноза верхнего уровня.

На макроуровне возможные варианты распределения функций ХТС между ее элементами определяются весовыми коэффициентами, учитывающими в вероятностном виде флуктуации среднего энергетического уровня подсистем (процессов) по отношению к уровню ХТС в целом, посредством макроэнтропии следующего вида:

,           ,                   (2)

где ni – значение весового коэффициента, N – число элементов в системе.

Весовые коэффициенты определяют вероятность флуктуации среднего

энергетического уровня процесса по отношению к уровню ХТС в целом.

 

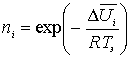,                                       (3)

где  – минимальная работа, необходимая для того, чтобы обратимым образом провести i-ое преобразование технологического потока,U0 – нулевой уровень отсчета, RTэ  – уровень энергии ХТС в целом.

В соответствии с постулатами информационно-термодинамического подхода и условием изоэнергетичности всех этапов преобразования информации для анализа взаимодействия подсистем на макроуровне используется понятие о замкнутой термодинамической подсистеме, границы контрольной поверхности которой не пересекают потоки вещества. Предел взаимодействия таких подсистем, находящихся внутри замкнутой системы, устанавливается на основании нулевого закона термодинамики в соответствии со стремлением к максимуму выражения (2).

Постановка задачи оптимизации по критерию макроэнтропии можно представить следующим образом:

 

                                 (4)

                                                           (5)

                                               (6)

 

Для поиска максимума функции (3), при наличии ограничений типа равенств (5) и (6), используется метод неопределенных множителей Лагранжа.

Оптимальное распределение весовых коэффициентов определяется по выражению:

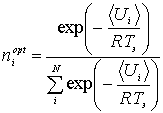,             .                   (7)

Исходя из принятой стратегии, задача оптимальной организации ХТС с реактором заключается в определении таких режимов работы реактора, которые удовлетворяли бы условию U i= idem, определенных из условия (7) для реактора.

Таким образом, задачу оптимальной организации целевого химического превращения вещества можно сформулировать следующим образом: для заданного оптимального вклада целевого превращения вещества в решении общей задачи организации ХТС, определяющего его средний энергетический уровень, найти параметры процесса химического превращения.

Поэтому задачей оптимизации 2 уровня является минимизация стоимости единицы информации для реактора при условии постоянства весового коэффициента. В качестве критерия оптимальности в данном случае будет выступать следующая величина:

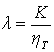,                                                      (8)

При этом

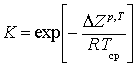, ,                               (9)

где ΔSр, ΔS0 – изменение термодинамической энтропии для реального и идеального процессов,  – изменение термодинамического потенциала Гиббса в процессе, Тср – средний температурный уровень.

Для поиска оптимального решения запишем систему уравнений следующего вида, определяющую температуры на входе и выходе из реактора (для случая адиабатического реактора без отвода теплоты):

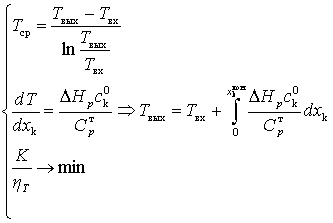                           (10)

Первое уравнение представляет собой ограничение по средней температуре процесса, второе уравнение – изменение температуры для адиабатического реактора, третье – условие минимизации стоимости единицы информации при постоянном  значении весового коэффициента целевого процесса.

Здесь  – средняя мольная теплоемкость смеси веществ при заданной температуре; Tнач, Tкон – начальная и конечная температура реактора,  – тепловой эффект реакции,  – начальная концентрация ключевого компонента;  – степень превращения ключевого компонента,  – конченая степень превращения ключевого компонента на выходе из реактора.

 

Литература

 

1.       Колесников, В.В. Принципы создания экотехнологий [Текст]/В.В Колесников, А.Ю. Налетов. - Москва: РХТУ, 2008. - 450 с.10.

2.       Налетов, В.А. Методика эволюционного синтеза химико-технологических систем на основе информационного подхода [Текст]/ В.А. Налетов, М.Б. Глебов, А.Ю. Налетов //Химическая технология. - 2010. - №4. - с.244-252.

3.       Налетов, В.А Информационно-термодинамический принцип организации химико - технологических систем [Текст]/ В. А. Налетов, Л.С. Гордеев, М.Б. Глебов, А.Ю. Налетов // Теоретические основы химической технологии ТОХТ. - 2011. - том 45, № 5. - с. 541–549.