Ванюлин Александр Николаевич – кандидат технических наук, доцент кафедры математических и инструментальных методов экономики. Чебоксарский Кооперативный институт (филиал) Российского университета кооперации. Россия, Чебоксары. E-mail: Van-U-Lin@yandex.ru.

 

ДИНАМИКА ЧИСЛЕННОСТИ НАСЕЛЕНИЯ

СОВРЕМЕННОЙ РОССИИ

Аннотация

В статье приводятся результаты моделирования динамики численности населения современной России. Предложена модель, описывающая  динамику численности населения. Ее характерной особенностью является наличие параметров, учитывающих коэффициенты рождаемости, смертности и периода воспроизводства. Произведенные с ее помощью расчеты показали хорошее соответствие расчетных и реальных данных.

Ключевые слова

Ключевые слова: демография, динамика численности, Россия, модель, прогнозы.

I. Введение

В течение последнего десятилетия складывающаяся в России демографическая ситуация стала сферой интересов не только государственных органов статистики и ученых демографов, но и многих общественно-политических организаций и правительственных кругов [1]. Внимание к этой проблеме остается повышенным и в настоящее время [2].

Связано это с необходимостью оценки возможных последствий протекающих демографических процессов. Такая оценка необходима для разработки возможных действий государства и общества с целью обеспечения своего дальнейшего существования и развития.

Основными проблемами являются старение население, внешняя и внутренняя эмиграция и депопуляции, т.е. с уменьшением численности. Так, согласно самым мягким прогнозам  2005-2008 годов, численность населения России к 2030 году может уменьшиться на 30-40 млн. человек.

II. Постановка задачи

Технологической основой для таких прогнозов являются регрессионные полиномиальные модели первой или второй степени [3]. Выбор нужной степени полинома производится исходя из требований адекватности описания процесса – соответствия расчетных и реальных данных по некоторым статистическим критериям.

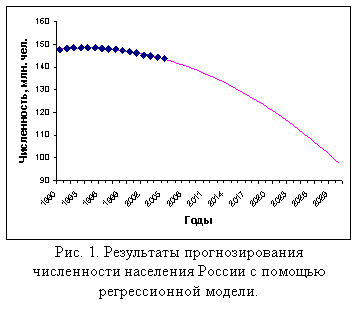
Действительно, если взять данные по численности населения России за 1990-2005 годы [7],  получить для них адекватную регрессионную модель второго порядка и сделать с ее помощью достаточно дальний прогноз, то действительно получаются указанные цифры – рис. 1.

В то же время известно, что регрессионные модели для прогнозов используются «не от хорошей жизни», а только в тех случаях, когда неизвестно математическое описание процесса (или это описание невозможно получить).

Целью настоящей работы является попытка получить более приемлемое математическое описание демографического процесса.

III. Результаты

С точки зрения математического моделирования демография представляет собой типичную динамическую систему, для описания которой можно использовать стандартный математический аппарат в виде дифференциальных уравнений или их систем.

При этом, практически в любой литературе, посвященной демографии (см. например [4]), указываются главные особенности динамики численности населения:

1. Величина убыли населения пропорциональна текущей численности.

2. Величина прироста населения пропорциональна не текущей численности населения, а той численности населения, которая была некоторое время назад.

Указанные моменты позволяют для описания демографического процесса предложить следующую модель:

 

            (1)

 

где     - изменение численности населения в момент времени t;

 - коэффициент рождаемости;

 - коэффициент смертности;

 - численность населения в момент времени ;

 - текущая численность населения (в момент  времени t);    

 - время запаздывания процесса. Этому параметру можно придать смысл периода воспроизводства человека.

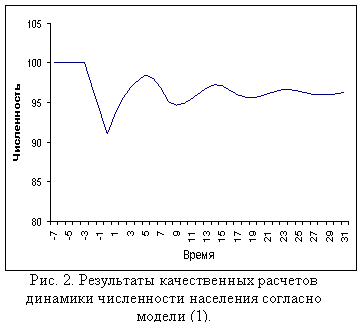
Качественное решение уравнения (1) в графическом виде представлено на рис. 1.

Решение получено при следующих условиях:

- в период с -7 по -3 годы от начала отсчета наблюдалась постоянная численность населения;

- в период с -2 по 0 годы наблюдалось существенное снижение численности населения;

- коэффициент рождаемости равен 0,3;

- коэффициент смертности равен 0,3;

- время запаздывания равно 8.

Как следует из рис.2 динамика численности представляет собой затухающий периодический процесс и постепенно превращается в прямую линию, параллельную оси времени. Очевидно, что стабилизация численности обусловлено равенством коэффициентом рождаемости и смертности.

Очевидно, что прямолинейная зависимость численности от времени является идеальной. Изменение численности населения любой страны никогда не представляются прямой линией. Объяснение очевидное - в истории всех стран хватает потрясений, во время которых часть населения либо гибнет, либо эмигрирует и, в результате, образуются новые демографические волны.

В России XX века имело место как минимум три таких потрясения: гражданская война, война 1941-1945 г.г. и так называемая перестройка 90-х годов.

Можно предположить, что на сегодня основной является волна, вызванная перестройкой. Ее последствия и ощущаются в настоящее время.

Остается только определить параметры этой волны и на их основе попытаться сделать прогнозы.

В предлагаемую модель входят три параметра:

- коэффициент рождаемости;

- коэффициент смертности;

- время запаздывания (период воспроизводства).

Для их определения были использованы стандартные методы, применяемые при обработке экспериментальных данных. Это, прежде всего, метод наименьших квадратов (МНК).

Результаты расчетов дают следующие значения параметров модели:

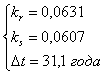                                                               (2)

Перед обсуждением полученных значений отметим следующий момент: очень большой удачей аналитика считается то, что полученные им характеристики будут хоть как-то согласовываться с реально имеющимися статистическими данными.

Все эти параметры должны быть усредненными для России и такое усреднение вполне целесообразно и оправдано для описания динамики численности такого большого объекта как Россия.

Обобщенные значения первых двух параметров (коэффициентов рождаемости и смертности) для России последних лет приведены в [7] .

Для периода 1990-2005 годов усредненное значение коэффициента рождаемости равно 0,0098, а коэффициента смертности равно 0,0145.

Cравнение полученных значений коэффициентов рождаемости и смертности со статистическими показывает, что они в 4-5 раз больше последних. Это может свидетельствовать о том, что в детовоспроизводстве участвует  примерно 20-25% населения. Очевидно, что основная часть этого населения приходится на возраст от 20 до 40 лет.

Повышенному риску смертности подвержен, примерно, тот же процент населения. И также очевидно, что основная масса населения участвующая в процессе смертности,  приходится на возраст от 50 лет и выше.

Надежных значений третьего параметров в литературе найти практически невозможно. Получившееся же его значение представляется вполне разумным.

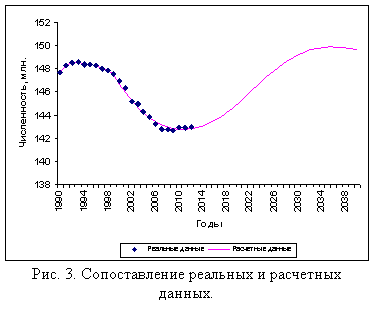
Сопоставление реальных и расчетных данных представлено на рис. 3.

К очень «дальним прогнозам» по любой, даже самой совершенной модели, можно относиться весьма скептически. Тем не менее, на этом же рисунке расчетные данные экстраполированы до 2040 г.  с целью демонстрации работоспособности модели.

Из расчетов следует, что очередной пик волны будет наблюдаться в 2035  г. (149,85 млн.) после чего начнется спад численности.

Для дополнительной проверки предлагаемая модель была использована для оценки потерь населения в результате Великой отечественной войны.

Дело в том, что в зависимости от степени ненависти к своей стране разные авторы приводят различные цифры этих потерь – от 16 до 44 млн. чел. [6].  Сейчас практически официальной считается цифра, равная 27 млн. чел.

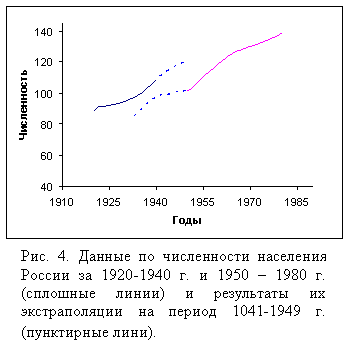
Имеющиеся данные по довоенной и послевоенной численности приведены на рис. 4 (сплошные линии).

 По обоим рядам данных были произведены аналогичные расчеты, которые дали следующие значения параметров:

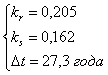              (3)

Отметим, что значения параметров существенно отличаются от (3):

- для данного периода значение коэффициента рождаемости существенно больше, чем для периода 2000-х годов. Это вполне объяснимо как большей многодетностью семей того времени;

- значение коэффициента смертности также заметно больше. Это также легко объяснить более низким уровнем здравоохранения того времени;

- средний период репродукции составляет 27 лет, что заметно меньше  31 года для 2000-х годов. И это легко объясняется современными семейными тенденциями.

На рис. 4 также приведены результаты обоих рядов данных. При этом предвоенные данные были экстраполированы с помощью уравнения (1), а послевоенные с помощью формулы 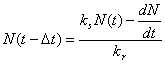(4):

     (4)

Отметим, что на обоих рядах четко прослеживаются те же демографические волны.

Если сопоставить экстраполированные данные для 1945 г., то разница составит 16,4 млн. чел. С учетом потерь Белоруссии, Украины и стран Балтии общие потери СССР в войне составят примерно 22 млн. чел., что заметно меньше официально признаваемой цифры.

IV. Выводы

Предложенная математическая модель позволила достаточно точно описать динамику численности населения России. Результаты расчетов хорошо совпадают с реальными данными о численности.

На основании этого совпадения произведены расчеты возможных потерь Советского Союза во второй мировой войне.

 

Список литературы

1.                 Выступление при представлении ежегодного Послания Президента РФ Федеральному собранию РФ, 8 июля 20005 года, Москва / Российская Федерация сегодня. 2005, №14.

2.                 Послание президента федеральному собранию 12 декабря 2013 года, http://www.rg.ru/2013/12/12/poslanie.html

3.                 Баранов А. Социально - экономические проблемы депопуляции и старения населения / Вопросы экономики. 2008, № 7

4.                 Демография. Учебник для вузов. / В.А. Борисов - М.: NOTA BENE, 2007.-344с.

5.                 Регионы России. Социально-экономические показатели в 2007 г. Стат. Бюллетень. / Росстат. - М., 2008.

6.                 Рыбаковский Л.Л., Людские потери СССР и России в великой отечественной войне, (Издание второе, исправленное и дополненное), Москва – 2010, http://rybakovsky.ru/demografia4.html

7.                 [http://ru.wikipedia.org/wiki]