К.ф-м.н. Макаричев А.В., Кудь А.А., Щукин А.Б.

Национальный аэрокосмический университет «ХАИ»

Харьковский национальный автомобильно-дорожный университет

СУММЫ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ПРИРАЩЕНИЙ В МОМЕНТ НАСТУПЛЕНИЯ РЕДКОГО СОБЫТИЯ

Пусть - последовательность независимых одинаково распределенных случайных величин с математическим ожиданием , и конечным вторым моментом , .

Обозначим сумму первых слагаемых

.

Пусть число слагаемых - случайная величина равная с вероятностью , где , .

Обозначим сумму случайных приращений в момент наступления некоторого события, вероятность наступления которого равна .

ТЕОРЕМА. При

.

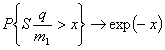Доказательство. Пусть - характеристическая функция для случайного приращения , . Найдем характеристическую функцию для случайной величины

.

Изучим асимптотическое поведение характеристической функции случайной величины . Имеем .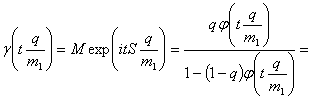

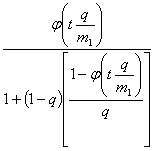При имеем

и ,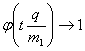

так как

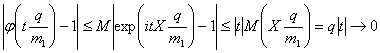
для любого .

Кроме этого,

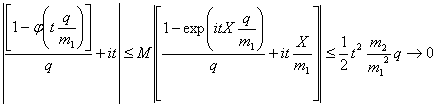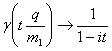при . Таким образом, при . Следовательно, при характеристическая функция случайной величины стремится к характеристической функции случайной величины, показательно распределенной с параметром 1. В силу обратной предельной теоремы для последовательностей функций распределения и последовательностей их характеристических функций при

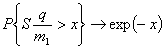
для любого , что и требовалось доказать. Теорема доказана.

Исходя из этой теоремы, при малых значениях можно приближенно вычислять вероятность

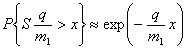
для любого .

Литература.

1. Гнеденко Б.В. Курс теории вероятностей, - 6 изд. - М., Наука, 1988.

2. Соловьев А.Д. Асимптотическое поведение момента наступления редкого события в регенерирующем процессе. Известия АН СССР. Техническая кибернетика, 1971, № 6, с. 79-89.

3. Ширяев А.Н. Вероятность, М.: Наука, 1980, 576 c.