К.т.н. Блохина В.Б,
к.ф-м.н. Павлова
М.Н., к.п.н., Черникова Н.В.
Таганрогский
политехнический институт – Филиал ДГТУ
Метод построения двусторонних
приближений к решению двойственной балансовой модели с учетом утилизации
вредных отходов
Модель, учитывающая утилизацию вредных отходов и описываемая системой уравнений
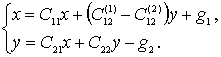 (1)
(1)
рассматривается
в Банаховом пространстве ![]() , полуупорядоченного конусом
, полуупорядоченного конусом ![]() [5]
[5]
где ![]() , причем операторы
, причем операторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() – положительные,
оператор
– положительные,
оператор ![]() не обязательно
положителен.
не обязательно
положителен.
Встала
задача: построить двойственную модель к модели (1) и определить оценки ее
решения, используя известный метод [4]. Задача была решена следующим образом.
Пусть ![]() ,
, ![]() – пространства
линейных ограниченных функционалов, сопряженные к пространствам
– пространства
линейных ограниченных функционалов, сопряженные к пространствам ![]() ,
, ![]() ;
; ![]() ,
, ![]() – сопряженные
полугруппы к конусам
– сопряженные
полугруппы к конусам ![]() ,
, ![]() соответственно;
соответственно; ![]() (
(![]() ) сопряженные операторы к операторам
) сопряженные операторы к операторам ![]() модели (1). При этом
модели (1). При этом
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В
рассматриваемой ситуации ![]() ,
, ![]() являются конусами
[3].
являются конусами
[3].
Модель вида
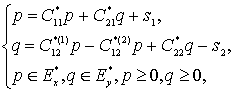 (2)
(2)
будем называть моделью, двойственной
к модели (1) [2]; [5].
Первое
уравнение этой модели означает, что цена полезного продукта является
справедливой, так как она состоит из стоимости затраченных полезных продуктов
(как в процессе производства, так и в процессе борьбы с загрязнением окружающей
среды) и добавленной стоимости, т.е. стоимости затраченного труда. Второе
соотношение модели (3) означает, что плата за создание одной единицы
загрязнения есть сумма стоимости затраченного на борьбу с загрязнением
полезного продукта и стоимости затрат на уничтожение воспроизводимого
загрязнения и затрат на утилизацию. В
случае, когда второе соотношение модели (3) будет выполнено со знаком
равенства, это будет означать, что назначенная плата за загрязнение является
справедливой. Если же второе соотношение будет выполнено со знаком неравенства,
то это будет говорить о том, что назначенная плата за загрязнение является
убыточной для общества в целом.
Модель (2) можно переписать в виде [4]:
![]() , (3)
, (3)
где 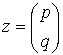 ,
, 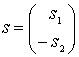 , С1
, С1![]() , С2
, С2![]()
Пусть ![]() – линейные операторы,
положительные в смысле М.Г. Клейна относительно конуса
– линейные операторы,
положительные в смысле М.Г. Клейна относительно конуса ![]() , где
, где ![]() ,
, ![]() – пространство
Банаха.
– пространство
Банаха.
Определение. Оператор ![]() называется монотонно
разложимым оператором, если он представим в виде разности:
называется монотонно
разложимым оператором, если он представим в виде разности:
![]()
где
![]() – монотонные
операторы.
– монотонные
операторы.
По
уравнению (3) построим новое уравнение
![]() , (4)
, (4)
где
![]() ,
, ![]() ,
, 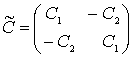 .
.
При
этом элемент ![]() можно рассматривать как элемент нового
пространства
можно рассматривать как элемент нового
пространства ![]() с нормой
с нормой ![]() , полуупорядоченного конусом
, полуупорядоченного конусом ![]() [3].
[3].
При
этом конус ![]() «наследует» основные
свойства конуса
«наследует» основные
свойства конуса ![]() (в частности,
(в частности, ![]() телесен, если телесен
конус
телесен, если телесен
конус ![]() ,
, ![]() – воспроизводящий,
если воспроизводящим является конус
– воспроизводящий,
если воспроизводящим является конус ![]() ,
, ![]() обладает свойством
нормальности, если нормален конус
обладает свойством
нормальности, если нормален конус ![]() и другие).
и другие).
Оператор
![]() оставляет
инвариантным конус
оставляет
инвариантным конус ![]() , а это значит, что оператор
, а это значит, что оператор ![]() положителен
относительно
положителен
относительно ![]() (последнее свойство
имеет место несмотря на то, что оператор
(последнее свойство
имеет место несмотря на то, что оператор ![]() имеет два
«отрицательных» блока). С помощью изложенной схемы можно сводить изучение
уравнений с монотонно разложимыми операторами к изучению вспомогательного
уравнения с оператором
имеет два
«отрицательных» блока). С помощью изложенной схемы можно сводить изучение
уравнений с монотонно разложимыми операторами к изучению вспомогательного
уравнения с оператором ![]() в новом пространстве
в новом пространстве ![]() ; при этом оператор
; при этом оператор ![]() является
положительным относительно
является
положительным относительно ![]() .
.
Построим для решения
уравнения (4) последовательные приближения
![]() , k = 0, 1, …
, k = 0, 1, …
c оператором ![]() , положительным относительно
, положительным относительно ![]() .
.
Для
решения уравнения (3)
![]()
воспользуемся
следующим методом [4],
![]() ,
, ![]() (n=0,1,2,…),
(n=0,1,2,…),
v0 и и0
таковы, что
![]() ,
, ![]() и
и ![]() .
.
Тогда
справедливы неравенства: ![]() (запись v £ и означает, что
компоненты вектора u
- v неотрицательны) и
последовательности
(запись v £ и означает, что
компоненты вектора u
- v неотрицательны) и
последовательности ![]() сходятся, а их
полусумма
сходятся, а их
полусумма ![]() сходится к решению
уравнения
сходится к решению
уравнения ![]() .
.
Теорема. Пусть оператор ![]() фокусирует с
постоянной c [1] и
фокусирует с
постоянной c [1] и
![]() ,
,
![]() .
.
Положим
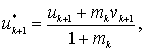
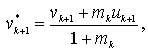
где
![]()
Здесь неотрицательные
параметры ![]() выбираются так, чтобы
на каждом шаге были выполнены соотношения
выбираются так, чтобы
на каждом шаге были выполнены соотношения
![]() ,
, ![]() .
.
Тогда
при выполнении условия ![]() имеют место
неравенства
имеют место
неравенства
![]()
и либо
метод сходится за конечное число шагов, либо верна оценка:
![]() .
.
Уместно
сравнить установленное выше неравенство
с известным неравенством [4]:
![]() ,
,
где
![]() – спектральный радиус
оператора
– спектральный радиус
оператора ![]() . Имея в виду это неравенство, можно сказать, что скорость
сходимости изучаемого метода ускорения сходимости близка к скорости убывания
геометрической прогрессии со знаменателем, имеющим, вообще говоря, порядок
величины
. Имея в виду это неравенство, можно сказать, что скорость
сходимости изучаемого метода ускорения сходимости близка к скорости убывания
геометрической прогрессии со знаменателем, имеющим, вообще говоря, порядок
величины ![]() , где
, где ![]() – второе по
абсолютной величине собственное значение оператора
– второе по
абсолютной величине собственное значение оператора ![]() .
.
Литература:
1.
Красносельский
М.А., Лифшиц Е.А., Соболев А.В. Позитивные линейные системы: метод
положительных операторов. – М.: Наука, 1985. – 256 с.
2.
Кремер Н.Ш., Путко Б.А.,
Тришин И.М., Фридман М.Н. Исследование операций в экономике: учебное пособие
для вузов / под ред. проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1997.
– 407 с.
3.
Петлина
Е.М. Развитие динамических межотраслевых моделей и математические методы их
анализа дис. ... к-та физ.-мат. наук. – Ставрополь, 2010. – 138 с.
4.
Стеценко
В.Я., Павлова М.Н., Кубекова Б.С. Об одном методе построения двусторонних
приближений к решению операторного уравнения с монотонно разложимым оператором
// Вычислительная математика и математическая физика. – 2001. – Т. 41. – № 6. –
С. 846–854.
5.
Стеценко В.Я., Сергеева Т.С., М.Н. Павлова
Модель межотраслевого баланса, учитывающая выделение вредных отходов и их
утилизацию. Математическое развитие модели.
(учебное пособие, Ставрополь СГУ, 2004, с.126