К.ф.-м.н. Трушин В.Б., д.п.н. Шомполов И.Г.

Московский физико-технический институт (государственный университет), Россия

Геометрическая интерпретация метода нормальных уравнений

В [1] решение системы линейных алгебраических уравнений (СЛАУ) методом нормальных систем сведена к решению операторного уравнения с монотонным отображением. Здесь мы уточним некоторые утверждения из [2].

Рассмотрим систему линейных алгебраических уравнений, имеющих единственное решение: . Здесь . Вместо исходной системы рассмотрим вспомогательную нормальную систему . Покажем далее, что метод нормальных систем имеет простую геометрическую интерпретацию, позволяющую делать перестройку матрицы системы для оптимизации численных решений.

Запишем СЛАУ в виде - вектор нормали плоскости , а – скалярное произведение векторов и .

Для каждого введем оператор .

Лемма 1. является непрерывным монотонным оператором.

Лемма 2. строго монотонный оператор, т.е.

.

Теорема 1. справедливо неравенство

,

Где 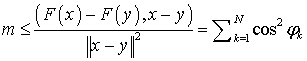и – угол между векторами и . При этом, если лежит в некотором конусе с вершиной в , то

,

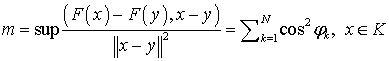и для улучшения сходимости следует добиваться увеличения числа за счет возможной перестройки матрицы исходной системы.

Рассмотрим итерационный процесс (ИП) .

Лемма 3. Пусть – решение исходной системы, элемент последовательности ИП, тогда при любом начальном элементе ИП выполняются неравенства

,

.

Теорема 2. Пусть – решение исходной системы, элемент ИП, тогда при 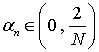, справедлива оценка , где , .

Оптимальным значением будет , . Экспериментально При ИП расходится. ИП для систем с большим числом обусловленности сходится медленно. Поэтому в процессе вычислений необходимо проводить продолжение решения по параметру.

Сходимость указанного ИП значительно улучшается, если вместо матрицы выбрать некоторую вспомогательную матрицу , у которой все скалярные произведения были бы положительными. Нормируем предварительно все векторы , т.е. далее считаем .

Действительно, если все скалярные произведения равны нулю, то матрица , поэтому и задача решается тривиально. Рассмотрим теперь случай, когда не все скалярные произведения равны нулю. Т.к. , то при утверждение справедливо. При возьмем линейную комбинацию векторов , а число 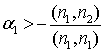, тогда обозначим как . Для наше утверждение доказано. Пусть утверждение справедливо для и докажем его для . Пусть векторы выбраны так, чтобы . Положим , 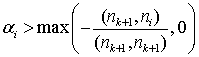рассмотрим скалярные произведения : .

Т.к. , то утверждение доказано по индукции полностью.

Теперь покажем, что только что изученная задача может интерпретироваться как геометрическое представление метода нормальных уравнений решения систем линейных алгебраических уравнений, а перестройки матриц дают методы улучшения сходимости метода нормальных уравнений. Запишем систему в векторном виде , где , тогда нормализованная система уравнений имеет вид , что эквивалентно векторному уравнению или операторному уравнению .

Литература:

1. Трушин Ю.В. Решение систем линейных уравнений с большим числом обусловленности при помощи одной задачи с монотонным оператором штрафа. Труды Института системного анализа Российской Академии Наук. Динамика неоднородных систем. Выпуск 10(1).-М.: КомКнига, 2005.-С. 193-203.

2. Трушин В.Б., Трушин Ю.В., Шомполова О.И. О монотонности и коэрцитивности одного отображения // Современные проблемы фундаментальных и прикладных наук / Программа 49 научной конференции МФТИ. - Москва-Долгопрудный, 2006.- С. 153.