Физика /3

к.т.н., доц. Фомин А.А., д.т.н., проф. Родионов И.В., студ. Фомина М.А.

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

Математическая модель кристаллизации микрослитков плазменного покрытия, полученного при индукционно-термической обработке металлической основы

Научные исследования проведены при финансовой поддержке грантов РФФИ № 13-03-00898 «а» и СП-1051.2012.4.

Структурообразование газотермических, в частности, плазменных покрытий с позиции теории кристаллизации микрослитков, включает в себя стадии нуклеации и роста закритических зародышей [1, 2]. При этом в зависимости от условий кристаллизации расплава напыленных частиц (микрослитков), происходит образование квазиаморфной и кристаллической структуры с нанометровыми зернами, а также более крупными образованиями, например, агломератами субмикрометровой или микрометровой величины [3].

Подтверждение выдвинутых положений предусматривает использование комплекса теоретических и экспериментальных исследований с применением методов электронно-микроскопического анализа структуры на примере керамических биосовместимых материалов на основе гидроксиапатита (ГА), полученных в виде плазменных покрытий с предварительной индукционно-термической обработкой (ИТО) титановой основы образцов.

Процесс затвердевания микрослитков при интенсивном охлаждении характеризуется двумя стадиями [1]:

1. Объемной кристаллизацией, заключающейся в образовании критических зародышей;

2. Ростом закритических зародышей до нанометровой, субмикрометровой или микрометровой величины.

Процесс кристаллизации протекает с переохлаждением фронта затвердевания, причем скорость его движения определяется тепловым балансом и частотой присоединения атомов жидкой фазы к кристаллической фазе.

Математическая модель начальной стадии процесса затвердевания включает в себя вероятностное уравнение Колмогорова, учитывающее нуклеацию и гомогенный рост кристаллических зерен:

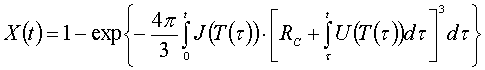, (1)

где t – длительность процесса кристаллизации, с; τ – текущая временная координата, с; Т – температура, K; Х – объемная доля закристаллизовавшегося вещества; J – частота образования критических зародышей в единице объема, 1/м³∙с; U – скорость роста кристаллов, м/с; R_C – критический радиус зародыша кристаллической фазы, м.

В рассматриваемом объеме расплава частицы параллельно протекают процессы образования критических кристаллических зародышей, а также их рост с последующим превращением в нанометровые или микрометровые зерна (рис. 1) [3].

Рассмотрим стадию закритического роста, которая в описывается известным дифференциальным уравнением [4]:

, (2)

Таким образом, в уравнении (2) скорость роста кристалла U определяется произведением эмпирических величин зернограничной подвижности m и поверхностной энергии зерна γ.

Рис. 1. Морфология микро- (а, б) и наноструктуры (в, г) покрытий ГА, полученных при различных режимах ИТО титановой основы

Интегрирование уравнения (2) приводит к следующему выражению:

, (3)

где R – радиус зерна, м; R_C – исходный размер зерна, в частном случае величина критического зародыша, м; t – длительность процесса кристаллизации, с; – структурная характеристика материала; n – эмпирический показатель степени, для поликристаллических материалов находящийся в диапазоне от 2 до 4; m – эмпирический параметр, характеризующий зернограничную подвижность, м⁴/(Дж∙с); γ – зернограничная энергия, Дж/м².

Перепишем выражение (3):

, (4)

В наиболее простом случае, при n = 2, выражение для определения среднего диаметра зерен (4) принимает явный вид:

, (5)

В выражении (5) необходимо определить исходный размер закритического кристаллита R_C [2]. Фундаментальная проблема перестройки атомной структуры расплава в процессе быстрого охлаждения остается актуальной и по сей день. При этом процессе происходит образование аморфной или аморфно-кристаллической структуры материала, и трудность описания этих превращений связана с отсутствием общепринятой теории структурной организации.

В случае сферического критического зародыша радиуса R_C , содержащего N_C атомов, имеем следующее выражение:

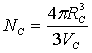, (6)

Исходя из эмпирических данных установлено, что число атомов в критическом кристаллическом зародыше (кластере) находится в пределах от 30 до 80. Радиус критического зародыша зависит от элементарного объема кристаллической решетки. Для решетки гексагональной сингонии P6₃/m примем допущение, согласно которому V_C ~ а³. Для ГА среднее значение параметра решетки а = 9,42 Å, определенное по справочным данным JCPDS карточек: 09-0432, 24-0033, 34-0010. Таким образом, при расчетах величины критического зародыша ГА из формулы (6) получаем R_C = 2,9…4,0 нм.

Возвращаясь к выражению (5), примем допущение, что процесс роста зерен является изотропным, тогда имеем следующую оценку:

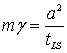, (7)

где t_LS – длительность процесса перехода атомов из расплава в кристаллическую фазу.

Обобщая данные полученных выше закономерностей (5), а также с учетом длительности процесса охлаждения t_ref , выражение для определения величины зерен принимает следующий вид:

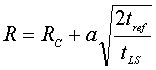, (8)

Чем быстрее атомы переходят из расплава в объем кристаллической фазы, тем интенсивнее протекает рост линейного размера зерна R. Длительность процесса охлаждения лимитирует рост зерна, при этом можно выделить две стадии:

1. Интенсивный рост зерен при t_ref << t_LS;

2. Элиминирование воздействия фактора роста зерен при t_ref → t_LS.

Зависимость размера зерна R от времени охлаждения t_ref при различной длительности кристаллизации t_ref представлена на рис. 2. Согласно предлагаемой теории закритического роста зерен, расчет показал, что для получения зерен нанометрового размера необходимо снижать длительность процесса охлаждения t_ref. При создании условий, способствующих увеличению продолжительности процесса перехода атомов из расплава в кристаллическую фазу t_LS до 10^-8…10^-10 с можно получать плазменные покрытия с аморфной, нанокристаллической и субмикрометровой структурой.

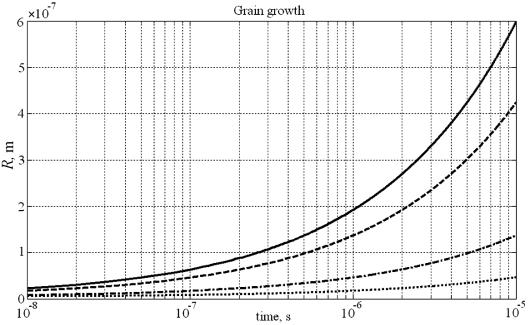
Рис. 2. Кинетика роста нанометровых и субмикрометровых зерен при различных значениях t_LS:

— - 5∙10^-11 с [2]; − − - 10^-10 с; − ∙ - 10^-9 с; ∙∙∙∙∙∙∙∙ - 10^-8 с

Литература

1. Ревизников Д.Л., Русаков В.В. Теплообмен и кинетика кристаллизации частиц расплава при интенсивном охлаждении // Математическое моделирование. 1999. Т. 11. № 2. С.55.

2. Евтеев А.В., Косилов A.T., Левченко Е.В., Логачев О.Б. Кинетика изотермической нуклеации в переохлажденном расплаве железа // Физика твердого тела. 2006. Т. 48. Вып. 5. С.769.

3. Fomin A.A., et al. Nanocrystalline Structure of the Surface Layer of Plasma-Sprayed Hydroxyapatite Coatings Obtained upon Preliminary Induction Heat Treatment of Metal Base // Tech. Phys. Letters. 2012. Vol. 38. № 5. pp. 481.

4. Rupp J.L.M., Infortuna A., Gauckler L.J. Microstrain and self-limited grain growth in nanocrystalline ceria ceramics // Acta mater. 2006. Vol. 54. pp. 1721.