Технические науки/2. Механика

К.ф.-м.н. Фоминых С.О.

Чувашский государственный педагогический университет им. И. Я. Яковлева, Россия

Упругопластическое состояние тел,

ослабленных концентратором напряжений

Предельное условие для напряжений в случае трансляционной идеальнопластической анизотропии для случая плоской деформации имеет вид [1]

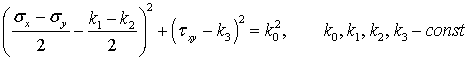, (1)

где - компоненты напряжения в декартовой системе координат, - предел текучести.

В дальнейшем все величины, имеющие размерность напряжения предполагаются безразмерными, отнесенными к величине предела текучести Компонентам напряжений в пластической зоне приписан индекс «p» наверху, компонентам в упругой зоне – индекс «е» наверху.

Условие (1) примет вид

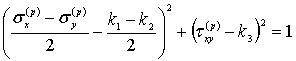. (2)

Согласно (2), анизотропия материала ориентирована в декартовой системе координат .

Связь между напряжениями в декартовой системе координат и напряжениями в полярной системе координат имеет вид

(3)

Из (2), (3) получим условие пластичности в полярных координатах

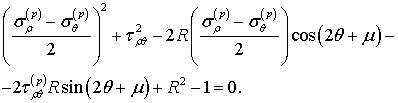(4)

где

, , .

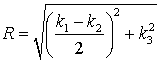Напряжения в пластической зоне имеют вид

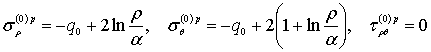. (5)

Решение в упругой области будем искать в виде

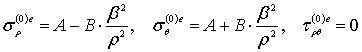. (6)

Условия сопряжения компонент напряжений на упругопластической границе имеют вид

(7)

Решение в пластической зоне имеет вид

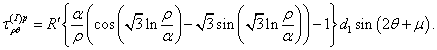(8)

Результирующее напряжение в упругой области имеет вид:

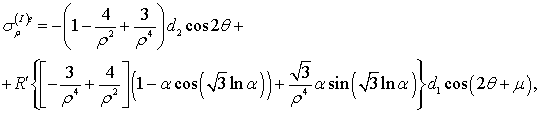
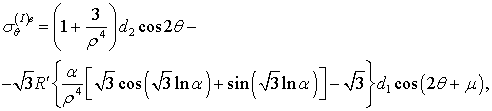
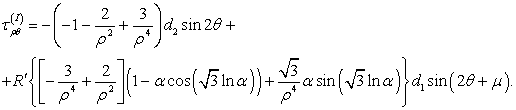(9)

Для определения границы раздела упругопластической области в первом приближении будем иметь

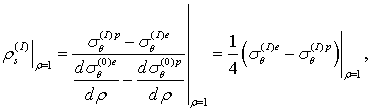(10)

откуда

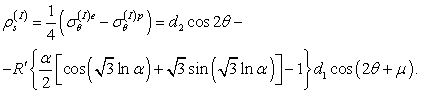(11)

Таким образом, напряженное состояние в пластической (9) и упругой (10) областях полностью определено. Изменение границы раздела упругой и пластической областей определяется из соотношения (11).

Литература:

1. Ивлев, Д. Д. О соотношениях теории трансляционной идеально-пластической анизотропии при обобщении условия пластичности Мизеса / Д.Д Ивлев, Л.А. Максимова // Вестник ЧГПУ им. И.Я. Яковлева. Серия: Механика предельного состояния. – 2010. - № 2(8). Ч.3. – С. 583-584.