К.т.н., Кузьменко А.А., Вагин Д.В., Колесниченко Д.А.

Институт компьютерных технологий и информационной безопасности Южного федерального университета

ПОСТРОЕНИЕ АЛГОРИТМОВ СИНЕРГЕТИЧЕСКОГО УПРАВЛЕНИЯ ТРЕХСЕКТОРНОЙ МАКРОЭКОНОМИКОЙ

За последние 20 лет в экономической теории выделились два базовых направления развития макроэкономики – традиционное (равновесное) и эволюционное [1]. Суть первого состоит в том, что переходные процессы в макроэкономике заканчиваются установлением устойчивого равновесия, т.е. паузой между переходными процессами служит устойчивое равновесие. В соответствии со вторым направлением – макроэкономика перманентно находится в состоянии динамического равновесия, т.е. паузой служит очередной переходной процесс. С точки зрения синергетики принципиального противоречия между этими направлениями нет [2] – в макроэкономике одновременно протекают несколько разноплановых переходных процессов: «быстрые» и «медленные». К «медленным» можно отнести процессы, обусловленные научно-техническим прогрессом и проявляющиеся в новых продуктах и услугах, технологиях повышения ресурсоотдачи и уменьшения ресурсо- и энергоемкости. «Быстрыми» традиционно считаются процессы, вызванные изменением конъюнктуры рынка, управляющими решениями, в т.ч. изменениями внутренней и внешней политики, и др. Отсюда следует, что экономика по завершении переходного процесса либо возвращается в первоначальное состояние, либо оказывается в новом состоянии [1]. В данной работе рассмотрена математическая модель трехсекторной макроэкономики как многосвязной нелинейной динамической системы и выполнено построение алгоритмов непрерывного управления.

Традиционно макроэкономика описывается моделью Солоу, но более адекватное описание макроэкономических процессов дает трехсекторная модель экономики, в которой выделяют три агрегированных продукта – предметы труда, средства труда и предметы потребления [1]. Каждый из трех выделенных секторов производит свой продукт: материальный (i=0) – предметы труда (топливо, электроэнергия, сырье и другие материалы), фондосоздающий (i=1) – средства труда (машины, оборудование, производственные здания, сооружения и т.д.), потребительский (i=2) – предметы потребления.

При формировании модели трехсекторной макроэкономики делают те же предположения, что и для односекторной модели Солоу [1]: 1) предполагается, что за каждым сектором закреплены основные производственные фонды (ОПФ) – объем используемого капитала в i-м секторе. В то время как трудовые ресурсы и инвестиции могут свободно перемещаться между секторами; 2) технологический уклад считается постоянным и задается с помощью линейно-однородных неоклассических производственных функций Кобба-Дугласа , где , – выпуск продукции и число занятых в i-м секторе соответственно; 3) общее число занятых в производственной сфере изменяется с постоянным темпом прироста ; 4) коэффициенты износа ОПФ и прямых материальных затрат секторов постоянны.

Таким образом, при сделанных предположениях, трехсекторная модель экономики имеет вид

(1)

здесь – доля занятых в i-м секторе от общего количества занятых L, – производство предметов труда (материалов); – производство средств труда (инвестиционных товаров); – производство предметов потребления, – основные производственные фонды в i-м секторе.

В модели (1) последнее выражение отражает распределение продукции материального сектора – материальный баланс. При данной стратегии управления управляющими воздействиями являются инвестиционные потоки в соответствующий сектор Инвариантами-аттракторами этой задачи управления являются:

1) материальный баланс:

; (2)

здесь – доли расходов материального сектора в соответствующих секторах;

2) желаемые значения основных производственных фондов материального и потребительского секторов:

. (3)

Желаемые значения могут быть рассчитаны в соответствии с прогнозными значениями расходования ресурсов и уровнями потребления продукции. Данные уровни устанавливаются в соответствии с государственной программой развития макроэкономики и, как правило, соотносятся с программами стимулирования развития ресурсодобывающих отраслей, стимулирования внутреннего потребления продукции и т.п.

Итак, задача управления формулируется следующих образом: необходимо синтезировать синергетические законы управления динамикой трехсекторной макроэкономики (1), которые обеспечивают выполнение инвариантов (2), (3). В соответствии с методом аналитического конструирования агрегированных регуляторов (АКАР) вводим инвариантные многообразия по числу каналов управления [2]. Так как на первом же этапе синтезы мы можем обеспечить выполнение желаемых инвариантов (2), (3), то задаем инвариантные многообразия в явном виде

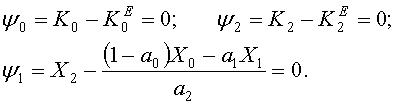(4)

Каждое из многообразий (4) должно удовлетворять решению основного функционального уравнения метода АКАР [2]:

. (5)

Уравнение вида (5) при асимптотически устойчиво относительно решения [2].

Из (5), с учетом (1) и (4), найдем законы управления:

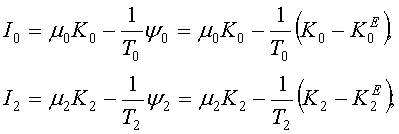(6)

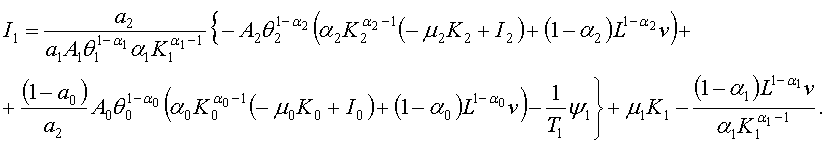
Управления (6) не содержат точек сингулярности, поскольку по условию в модели трехсекторной макроэкономики и . Эти управления обеспечивают перевод трехсекторной макроэкономики в стационарное состояние, определяемое желаемыми инвариантами (2), (3). Устойчивость системы (1) с синергетическими алгоритмами управления (6) определяется условием Проведем компьютерное моделирование системы (1) с синергетическими стратегиями управления (6) при этом исходные параметры системы (1) получены из данных официальной статистики РФ за 1960-1998 гг. [1]: а параметры законов управления: .

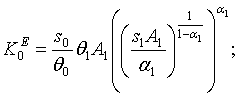
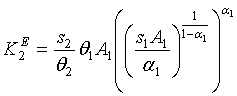Результаты моделирования представлены на рис. 1–4.

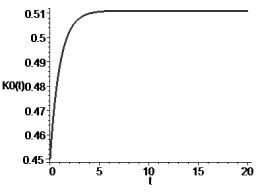
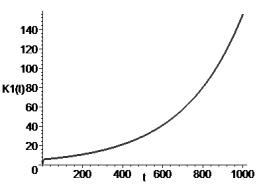
Рис. 1 – График изменения ОПФ в материальном секторе	Рис. 2 – График изменения ОПФ в фондосоздающем секторе
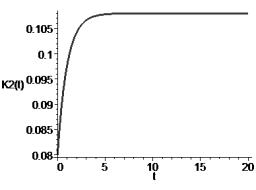
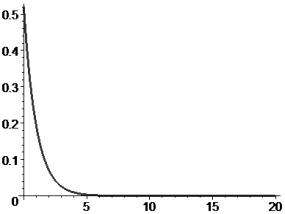
Рис. 3 – График изменения ОПФ в потребительском секторе	Рис. 4 – График изменения материального баланса

Из рис. 1, 3 видно, что обеспечивается выполнение инвариантов (3), а из рис. 4 – инварианта (2). Инвестиционные потоки в материальных и потребительский сектора стабилизируются, а в фондосоздающем изменяются линейно, стимулируя выпуск средств труда. Используя соответствующие информационные системы по алгоритмам управления (6) мы сможем оперативно определять величины инвестиций в соответствующие сектора экономики.

Литература

1 Колемаев В.А. Экономико-математическое моделирование. Моделирование макроэкономических процессов и систем. – М.: ЮНИТИ-ДАТА, 2005.

2. Колесников А.А. Синергетические методы управления сложными системами: Теория системного синтеза. Изд. 2, испр. –М.: ЛиброКом, 2012.