к.т.н. Куликов В.Ю., к.т.н. Саркенов Б.Б., Нурланов Р.С.

Карагандинский государственный технический университет, Казахстан

РАЗРАБОТКА МОДЕЛИ НЕЛИНЕЙНОГО НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ

ПЕСЧАНО-СМОЛЯНОЙ СМЕСИ

 

Главными составляющими формовочной песчано-смоляной смеси являются кварцевый песок и смола). Формирование прочной оболочки связано с физико-химическими процессами, происходящими в песчано-смоляной смеси при тепловом воздействии и статическом давлении. Подобные смеси имеют широкое применение, к ним относятся формовочные смеси, брикеты руд и угля.

Нелинейная деформация песчано-смоляной смеси в условиях объемного обусловлена, в основном, различным характером зависимости упругой, вязкой и пластической деформации от напряжения. Упругая деформация εу зависит от напряжения линейно, а пластическая εп и вязкая εв (зависят от вязкости связующего, в том числе и величины и скорости нагрева дисперсной смеси) связана с напряжением σ нелинейно. Известно, что составляющую вязкой части деформации можно определить из дифференциального уравнения (1)

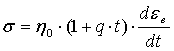                                                 ,                                           (1)

где η0 – коэффициент объемной вязкости; q – постоянная вязкости песчано-смоляной среды, t – время, прошедшее от начала деформации смеси.

              Так как нагрузка в смеси статическая и нагружение в целом производится с постоянной скоростью, то зададимся граничным условием =const. Тогда, проведя разделение переменных и, проинтегрировав каждую часть, получим вязкую составляющую

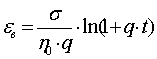                                                  .                                              (2)

          Аналогичным образом определим пластическую составляющую

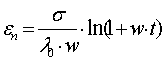                                                   ,                                           (3)

где λ – коэффициент пластичности, w – постоянная пластической части песчано-смоляной среды.

В таком случае закон деформирования смеси при воздействии статической нагрузки можно представить  следующей зависимостью (4):

                              ε=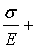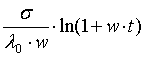+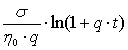,                           (4)

где Е – модуль упругости. Индекс ноль показывает, что данный коэффициент определяется в момент времени t=0.

                                    Обозначим  λ0·w=Е/а, η0·q=Е/b.Тогда

                   .            (5)

          Обозначим σ·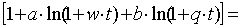σф,             (6)

где σф – напряжение, которое следовало бы приложить к дисперсной песчано-смоляной среде с модулем упругости Е в случае линейного деформирования для того, чтобы вызвать деформацию, равную получаемой от фактического напряжения σ у дисперсной среды, деформирующейся нелинейно с модулем упругости Е, модулем пластичности λ0 и коэффициентом вязкости η0.

          В неравновесном состоянии напряжение уравновешивается упругим и вязкопластическим и сопротивлением. Отсюда:

                        σф=σ·Е·ε+Е·τ·,                             (7)

где ε – неравновесная деформация; Е·τ – линейная вязкость.

         В начальный момент времени до воздействия на смесь статической нагрузкой (t=0). Таким образом, можно записать:

                            Е0ε0+Е0τ0·=σ0                                                    

                        Е1ε1+Е1τ1·=σ1·.                            (8)                            

Решение проведем аналогично, как показано в [1]. В результате совместного решения системы относительно ε, где ε=ε0+ε1, и принимая, что нагружение смеси осуществляется с постоянной скоростью, тогда: =const, dσ/dt=, σ=·t получаем следующее дифференциальное уравнение:

Е0 ·Е1 ·τ0­ ·τ1·+Е0 ·Е1 ·(τ0­+τ1)·+Е0 ·Е1 ·ε=

=[Е0 ·τ0+Е1 ·τ1+Е0·τ0·(1+a1·lnC+b1·lnD)+E1·τ1]+

                                 +[Е0+Е1+Е0 ·(1+a1·lnC+b1·lnD)+Е1]·σ.                                      (9)

         Общим решением этого уравнения является функция

                                        ε=В1t+B2,                                            (10)

         Находим корни этого уравнения и постоянные интегрирования при а1=а0=b1=b0=0 находим частные значения и получаем

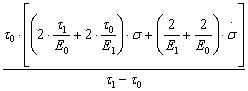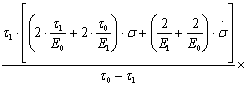
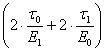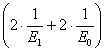ε=·+                                    +·σ+·.                              (11)

         Определим величину напряжений при ползучести песчано-смоляной смеси. Так как σ=const, то =0 и с учетом τ0=0, получим из уравнения (11)

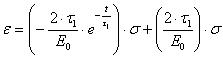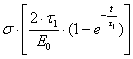                           =.                       (12)

         Зависимость (12) есть уравнение ползучести песчано-смоляной смеси при приложенной статической нагрузке на смесь.

Построение моделей, описывающих поведение песчано-смоляных смесей под воздействием разных факторов позволит ещё расширить границы использования этих смесей.