Хомченко А. Н.

Черноморский государственный университет им. Петра Могилы,
г. Николаев, Украина

МЕТОД УАЧСПРЕССА И КОНЕЧНОЭЛЕМЕНТНЫЕ АППРОКСИМАЦИИ.

Введение. В работе рассматриваются сложные модели конечных элементов (multiplex по определению Дж. Одена [1]). Основное внимание уделяется элементам, образующим серендипово семейство (Эргатудис, Айронс, Зенкевич [2]). Эти элементы часто называют изопараметрическими. Геометрический метод конструирования интерполяционных базисов (product of planes) был разработан Уачспрессом в начале 70-х годов прошлого века [3]. Метод в основном применялся на элементах в форме полигона (пентагон, гексагон и т.п.) и часто приводил к дробно-рациональным базисам, которые менее предпочтительны по сравнению с полиномиальными. Судя по публикациям Уачспресса и его последователей, в серендиповых аппроксимациях метод не применялся, хотя серендиповы элементы уже были известны с 1968 г. Начиная с 1982 г. автор приобрёл определённый опыт конструирования (по Уачспрессу) полиномиальных серендиповых базисов [4; 5]. Правда, классическая процедура product of planes теперь превратилась в product of surfaces, в которой плоскость рассматривается как частный случай поверхности, что вполне естественно. Примечательно, что, используя только плоскости, можно построить множество альтернативных серендиповых моделей. Если бы они появились в начале 70-х годов прошлого века, то в теории серендиповых аппроксимаций было бы значительно меньше заблуждений, ошибок и парадоксов [6].

Основная часть. Возможности метода Уачспресса и его модификации проиллюстрируем на примере элемента бикубической интерполяции Q12 [7] c 12-ю узлами равномерно расположенными по периметру квадрата (рис. 1).

Регулярно расположенные узлы интерполяции имеет следующие координаты: – угловые узлы; – промежуточные узлы на сторонах квадрата.

Как известно, интерполяционный полином имеет следующий вид:

, (1)

где – известные узловые значения функции. Задача сводиться к построению базиса, который состоит из 12-ти функций , обладающих следующими свойствами:

, (2)

где, – номер функции, – номер узла.

1 модель	2 модель	3 модель
4 модель	5 модель	6 модель

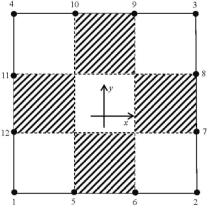
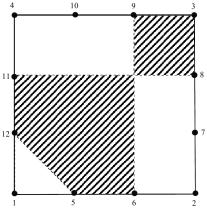
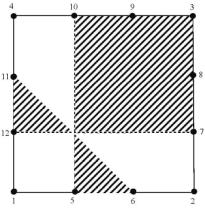
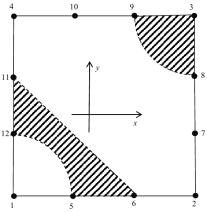
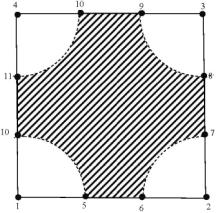
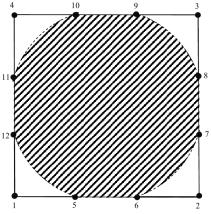
Рис. 1 Линии нулевого уровня
и области отрицательных значений (заштрихованы).

Как правило, «угловые» поверхности имеют более сложный рельеф по сравнению с «промежуточными». Это подтверждают линии нулевого уровня (рис. 1). Поэтому мы начинаем с . «Промежуточные» функции (например ) можно найти, пользуясь интерполяционной гипотезой (2). Как показывают портреты линий нулевого уровня , первые три модели можно сконструировать классическим методом Уачспресса, остальные три потребуют упомянутой выше модификации. Опишем подробнее процедуру построения для 3-й модели. Напомним, что все используемые плоскости должны проходить через точку . Чтобы идентифицировать конкретную плоскость достаточно назвать ещё две точки на границе элемента.

Уравнения плоскостей, проходящих через узлы:

Перемножение даёт:

(3)

Остальные «угловые» функции легко получить из (3). «Промежуточные» получаются из (2). Например,

(4)

из (4) легко получить остальные «промежуточные» функции.

Из второй группы моделей возьмем 6-ю, которая была получена подбором в 1968 г. [2] и до 1982 г. [4] считалась единственной моделью, реализующей бикубическую интерполяцию. Для построения 6-й модели нам потребуются две плоскости и и параболоид вращения . Перемножение даёт:

(5)

Для «промежуточной» функции получаем

(6)

Чтобы построить поверхность 4-й модели потребуются три плоскости и один гиперболический параболоид (гипар). Поверхность
5-й модели образуется перемножением двух плоскостей и двух гипаров.

Литература:

1. Оден Дж. Конечные элементы в нелинейной механике сплошных сред / Дж. Оден. – М. : Мир, 1976. – 464 с.

2. Zienkiewicz O. C. The Finite Element Method / O. C. Zienkiewicz, R. L. Taylor. – V. 1. – Butterworth-Heinemann, 2000. – 689 p.

3. Wachspress E. L. A Rational Finite Element Basis / E. L. Wachspress. – Press; New York, 1975. – 344 p.

4. Хомченко А. Н. О базисных функциях МКЭ для уравнений в частных производных / А. Н. Хомченко // 3-й Респ. симпозиум по диффер. и интегр. уравнениям: Тез. докладов. – Одесса, 1982. – С. 257-258

5. Хомченко А. Н. Геометрия полиномиальной интерполяции метода конечных элементов / А. Н. Хомченко // Прикладная геометрия и инженерная графика. – К. : КИСИ, 1987. – Вып. 43 – С. 80-82.

6. Астионенко И. А. Серендиповы аппроксимации: поучительные ошибки и контрпримеры / И. А. Астионенко, Е. И. Литвиненко, А. Н. Хомченко // Научные ведомости Белгород. гос. ун-та. Математика. Физика. – № 11 (130). Вып. 27. Белгород: Бел ГУ. 2012. – С. 110-115.

7. Akin J. E. Finite Element Analysis with Error Estimators / Butterworth-Heinemann, 2005. – 477 p.