Физика /1.Теоретическая физика

Ястребов А.Ю.

Государственный морской университет имени адмирала Ф.Ф.Ушакова ,

Россия

Энергетические зоны в кристаллах

Энергетические зоны. Химическую связь и свойства кристаллических тел можно объяснить с использованием метода молекулярных орбиталей. Согласно этому методу при образовании химической связи образуются молекулярные орбитали, охватывающие всю молекулу, причем происходит расщепление энергетических состояний на связывающие молекулярные орбитали с низкой энергией и разрыхляющие молекулярные орбитали с более высокой энергией.

При взаимодействии большего числа электронов атомов образуется соответственно и большее число молекулярных орбиталей и уменьшается разность энергий между ними (рис.1).

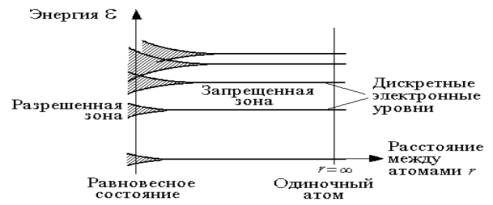
Рисунок 1. -Типичная схема образования энергетических зон.

При образовании кристаллов в химические связи вступает огромное число частиц N и соответственно образуется огромное число молекулярных орбиталей, охватывающих весь кристалл, разность между энергетическими уровнями молекулярных орбиталей чрезвычайно мала. В результате образуются энергетические зоны, состоящие из огромного числа подуровней (рис.2).

Рисунок 2. - Модели Кронига-Пенни.

Разность между верхней и нижней энергиями зоны называется шириной зоны. Например, если ширина зоны составляет 1 эВ, а в кристалле содержится 1 моль частиц, то разница между энергиями будет иметь порядок 10-21 кДж.

В изолированном атоме электроны способны занимать лишь дискретные энергетические уровни, определяемые силами притяжения к ядру и силами отталкивания от других электронов.

В результате из каждого дискретного энергетического уровня атома или молекулы образуется энергетическая зона, состоящая из очень близко расположенных энергетических уровней.

Типичная схема образования энергетических зон. Дискретные уровни одиночного атома расширяются в энергетические зоны по мере уменьшения межатомных расстояний в кристалле.

По мере сближения атомов сначала расщепляются самые высокие энергетические уровни, затем по мере сближения атомов – более низкие.
Самую верхнюю из зон, частично или полностью заполненную электронами, называют валентной зоной, а ближайшую к ней незаполненную электронами – зоной проводимости.

С точки зрения зонной теории все твердые тела можно подразделить на две основные группы: материалы, у которых валентная зона перекрывается зоной проводимости, и материалы, у которых валентная зона и зона проводимости разделены запрещенной зоной.

Материалы, в энергетической диаграмме которых запрещенная зона минимальна, относятся к проводникам, материалы с узкой запрещенной зоной (менее 3 эВ) – к полупроводникам, материалы с широкой запрещенной зоной (более 3 эВ) – к диэлектрикам.

Электроны, находящиеся на этих уровнях, приобретают способность перемещения по кристаллу. В модели Кронига-Пенни решеточные потенциалы периодической последовательностью прямоугольных потенциальных ям глубиной U и шириной а, разделенных потенциальными барьерами шириной b, так что постоянная решетки равна a + b.

Энергия электрона при этих условиях также квантуется по периоду решетки: ξ= ;

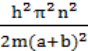где h=6.62* ��=3.14, n = 1,2,3… , m=9.1*[кг].

Стационарные состояния электрона описываются квазиимпульсом P = hq, аналогичным импульсу частицы в свободном пространстве при условии

q = p n/(a+b).

Таким образом, модель предсказывает серию дискретных уровней, которые соответствуют уровням частицы “в ящике”. В таких условиях электрон можно рассматривать находящимся внутри одной ячейки, хотя и невозможно установить, в какой именно. Электрон обладает квазиимпульсом P = hq и энергией e, которые являются периодической функцией в пространстве волновых векторов (q- пространство): e (q) = e (q + g) , где g - векторы обратной решетки abc. В качестве элементарной ячейки обратной решетки выбирают первую зону Бриллюэна.

Научный руководитель: к.п.н., доцент С.А.Мищик

ЛИТЕРАТУРА:

1. Бенуэлл К. Основы молекулярной спектроскопии: Пер. с анг. М.: Мир, 1985. — 384 с.

2. Вихман Э. Квантовая физика. – М.: Наука, 1974. — 391 с.

3. Савельев И.В.  Курс физики. т.3. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц.  М.: Наука. Гл. ред. физ.-мат. лит., 1989.—304 с.