Correction of electric signals transmitted on
damaged cable lines
Mayilov R.A., Mehdiyeva A.M.,
Khanmammadova E.A.
Azerbaijan State Oil and Industrial University, Baku,
Azerbaijan
e-mail:dadashovaelmira@mail.ru
Electromagnetic
energy spreads along cable line, decreases on value from the beginning to the
end of the line. Decreasing or attenuation of energy is explained by its losses
in the circuit of transmission and is taken into consideration by means of
coefficient of spreading. The ratio of current and voltage at the beginning and
in the end of the line expressed so:
![]()
The module of this
equation ![]() characterizes the decreasing of absolute
value of current or voltage at passing through lines with length l. Angle φ characterizes the changing of vector’s angle of current and
voltage at this part of line with the length L and shows changing of phase at
energy spreading in circuit.
characterizes the decreasing of absolute
value of current or voltage at passing through lines with length l. Angle φ characterizes the changing of vector’s angle of current and
voltage at this part of line with the length L and shows changing of phase at
energy spreading in circuit.
It is obvious, that the longer is cable line,
the bigger is changing of transmitted energy (signals of communication) on
value and phase.
When transmitting
signals of communication the parameters φOИ and φOI characterize correspondingly attenuation
and changing of phases of current, power and voltage at part of cable circuit
by length 1 km. Coefficient of spreading at the same time defines changing of
signal both on absolute value and on phase at 1 km of cable length.
Considerably
more complex electromagnetic processes appear in disuniform lines at disco
ordinated loads., where only part of energy comes to receiver and it is
absolute value less than at coordinated load:
![]() (1)
(1)
Qualitative characteristics of signal which
is transmitted by such cable line will be caused not by own attenuation of the line a = αl, but its working attenuation ap quantitative ratio
between energy applied to the receiver and reflected energy depends on ratio of
resistances of receiver and wave impedance ZB
and is characterized by coefficient of reflection: ![]() ,
,
 0251670528251659264251660288251662336251663360251664384251665408251666432251667456251668480251669504Working attenuation
aw is attenuation of cable circuit in working conditions and is calculated
by the equation:
0251670528251659264251660288251662336251663360251664384251665408251666432251667456251668480251669504Working attenuation
aw is attenuation of cable circuit in working conditions and is calculated
by the equation:  (2)
(2)
Where ![]() and
and ![]() .
.
These
are the coefficients of reflection at junction “generator-cable” and
“receiver-cable”. The later equation consists of four components. The first on
expresses own attenuation of cable αl;
the second and the third – attenuation because of disco ordination of
resistances of generator and cable Z0
≠ ZB, and also
of receiver and cable Zl ≠ ZB, the fourth component is
equal of attenuation from interaction of disco ordinations at the beginning and
in the end of the line.
When
coefficient of reflection is known, one can calculate wave impedance and
therefore define three last components in equation (2) and naturally working
declination. So, the ratio of current and voltage at the beginning and in the
end of the line, according to equation (1), will be as:
![]() and then
and then ![]() (3)
(3)
where, ![]() - values of voltage
and current in the ends of line in case of breaking of non-uniformity of lines.
Dividing (3) on (1) we will get next ratio
- values of voltage
and current in the ends of line in case of breaking of non-uniformity of lines.
Dividing (3) on (1) we will get next ratio
![]() (4)
(4)
Taking
into account the results of ratios in last equations, we will define value of
correction coefficients for calculation of real value of ![]() : So, defining the
own and the working attenuation of lines allows calculating real value of the
voltage and the current in the end of the line. Taking above discussed into an
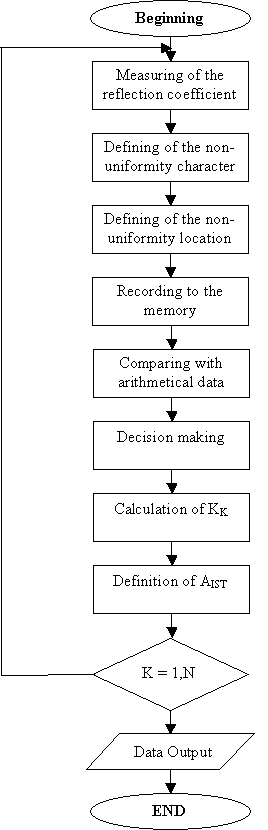
algorithm of measurement results correction is proposed.
: So, defining the
own and the working attenuation of lines allows calculating real value of the
voltage and the current in the end of the line. Taking above discussed into an
algorithm of measurement results correction is proposed.
Literature
1.
Былина М.С., Глаголев
С.Ф. Использование «биимпульса» в импульсной рефлектометрии. Тезисы докладов 58
НТК ГУТ, 2006.
2.
Былина М.С., Глаголев
С.Ф. Определение характера повреждения или неоднородности по рефлектограмме
кабельной цепи. Труды учебных заведений связи № 168, СПб, 2002. - 11 с.
3. Mailov R. A.“On
decision making of transmission information on cables of connection with
violated homogeneities.” Information conference 1999, Ulyanovsk, Russia.
Адаптивный
подход определение места и характера повреждений кабельных линий
Rauf Mayilov., Quliyev E. Aliyeva L.A.,
Elmira Khanmammadova.,
Azerbaijan State Oil and Industrial University, Baku, Azerbaijan
e-mail:dadashovaelmira@mail.ru
Как известно при импульсном методе
исследования кабельных линий по форме и временному расположению посланного и
отраженного сигналов судят о наличии повреждения в той или иной секции
многосекционного кабеля. При импульсном методе, использованном в разработанных
устройствах, из-за сильной подверженности воздействию помехи отраженный сигнал
существенно искажается как по амплитуде, так и по времени. Именно в таких
условиях неопределенности, т.е. в условиях отсутствия априорной информации о
наблюдаемых ситуациях целесообразно использование подходов адаптивного обучения .
Известно, что принцип работы обучающихся систем основан на использовании
процессов обучения, позволяющих в результате обработки текущей информации,
содержащейся в реализациях, восполнить недостаток начальной априорной
информации на основе вероятностных итеративных алгоритмов. При этом задача
обучения сводится к задаче классификации или распознавания образов, суть
которой сводится к построению поверхностей, разделяющих гиперпространство на
конечное число областей (секций кабеля), каждая из которых имеет свой образ.
Рассмотрим
функцию разбиения ![]() где
где ![]() - характеризует свойство анализируемой
конфигурации (неполадки в отдельных секциях кабеля). В качестве вектора
используется совокупность элементов
- характеризует свойство анализируемой
конфигурации (неполадки в отдельных секциях кабеля). В качестве вектора
используется совокупность элементов ![]()
![]() , где
, где ![]() – число секций
кабеля. Класс, в котором содержится конфигурация, обозначен через
– число секций
кабеля. Класс, в котором содержится конфигурация, обозначен через ![]() . В реальной обучающейся системе
. В реальной обучающейся системе ![]() будет
соответствовать различным сдвигам посылаемого сигнала, а у – отраженному сигналу, который надо
сопоставить с
будет
соответствовать различным сдвигам посылаемого сигнала, а у – отраженному сигналу, который надо
сопоставить с ![]() и определить номер секции, где имеется
неисправность. Для решения этой задачи составим аппроксимирующую функцию в
виде:
и определить номер секции, где имеется
неисправность. Для решения этой задачи составим аппроксимирующую функцию в
виде:
![]()
![]() Здесь
Здесь ![]() – линейно независимые, взаимно ортогональные функции, а
– линейно независимые, взаимно ортогональные функции, а ![]() ,
, ![]() – коэффициент аппроксимирующей функции.
– коэффициент аппроксимирующей функции.
Цель
обучения определяется ошибкой аппроксимации, которая оценивается с помощью
функционала:
![]()
где ![]() - строго выпуклая функция.
- строго выпуклая функция.
Поскольку
в качестве функции наиболее часто используется квадрат отклонения, градиент
будет определяться следующим образом:
![]()
При этом
непрерывный алгоритм обучения имеет следующий вид :
![]()
Здесь ![]() – параметр, учитывая лучшие значения , а параметр, учитывающий
скорость схождения;
– параметр, учитывая лучшие значения , а параметр, учитывающий
скорость схождения; ![]() - посылаемый сигнал;
- посылаемый сигнал; ![]() - отраженный непрерывный сигнал;
- отраженный непрерывный сигнал; ![]() - аппроксимирующая функция, зависимая от вектора независимых
параметров;
- аппроксимирующая функция, зависимая от вектора независимых
параметров; ![]() - вектор взаимоортогональных
функций (состоит из
- вектор взаимоортогональных
функций (состоит из ![]() ), где
), где ![]() – время задержек отраженного сигнала в одной секции кабеля.
– время задержек отраженного сигнала в одной секции кабеля.
С учетом вышеизложенного, алгоритм обучения для
непрерывного случая можно представить в следующем виде: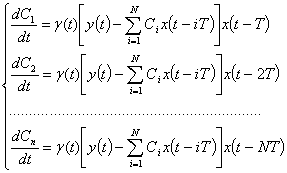
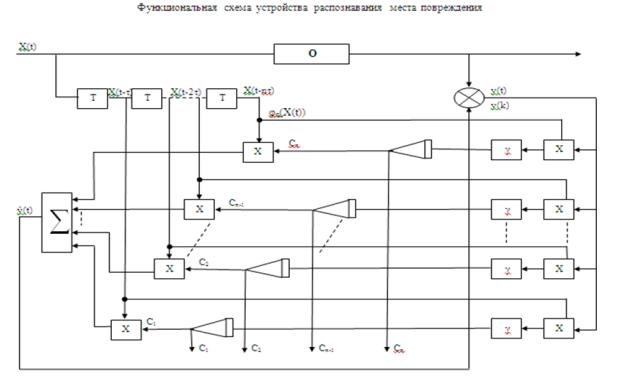
Функциональная
схема устройства для распознавания места повреждения в многосекционном кабеле
на основе предложенного алгоритма
представлена на рисунке. Устройство состоит из следующих блоков:
·
задержки посылаемого
сигнала за время ![]() для получения взаимоортогональных
функций;
для получения взаимоортогональных
функций;
·
выработка значений ![]() ;
;
·
интеграторов;
·
перемножения и
сумматоров.
Выходные сигналы соответствующих
интеграторов соответствуют коэффициентам
![]() ,
, ![]() и показывают номера секций, где имеются повреждения.
и показывают номера секций, где имеются повреждения.
Для дискретных сигналов, каковыми являются
импульсные, этот же алгоритм обучения будет иметь следующий вид:
Литература
1.Цыпкин Я.
З.Адаптация и обучение в автоматических системах - Москва : Наука, 1968. - 399 с
2.Былина М.С., Глаголев С.Ф. Определение характера
повреждения или неоднородности по рефлектограмме кабельной цепи. Труды учебных
заведений связи № 168, СПб, 2002. - 11 с.