Романюк В. В.
Хмельницький
національний університет
Про порядок перебору чистих стратегій в одній матричній грі без сідлової
точки для реалізації оптимальних змішаних стратегій
Теорія ігор і, зокрема, матричних ігор знаходить
своє застосування у багатьох галузях — в економіці, у сільському господарстві,
політиці, військовій справі тощо. Тому дослідження конфлікту є одним з
актуальних завдань прикладної математики. Розглянемо матричну ![]() -гру з симетричною додатною матрицею виграшів
-гру з симетричною додатною матрицею виграшів
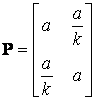 , (1)
, (1)
де ![]() ,
, ![]() . Оскільки
. Оскільки ![]() , то у цій грі її нижнє значення
, то у цій грі її нижнє значення
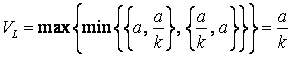 , (2)
, (2)
а верхнє значення
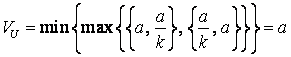 , (3)
, (3)
тобто ![]() , і множина сідлових точок є пустою.
, і множина сідлових точок є пустою.
Знайдемо оптимальні змішані стратегії першого ![]() та другого
та другого ![]() гравців у цій грі.
Матриця (1) є симетричною,
гравців у цій грі.
Матриця (1) є симетричною, ![]() , отже,
, отже, ![]() і очевидно, що
і очевидно, що
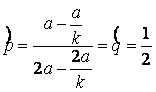 . (4)
. (4)
Тепер маємо оптимальні змішані стратегії ![]() , застосування яких у грі з симетричною додатною матрицею (1)
гарантує очікуваний виграш першому гравцю (очікуваний програш другому гравцю)
, застосування яких у грі з симетричною додатною матрицею (1)
гарантує очікуваний виграш першому гравцю (очікуваний програш другому гравцю)
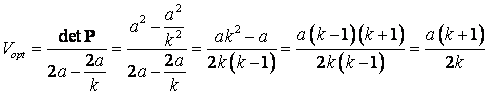 . (5)
. (5)
Але перший гравець гарантовано отримає такий виграш тільки при використанні
оптимальної змішаної стратегії ![]() , що теоретично можливо лише при нескінченному повторюванні
цієї гри. Натомість на практиці, коли моделлю реальної ситуації є матрична гра,
кількість повторювань гри завжди обмежена. Тому виникає проблема реалізації
оптимальних змішаних стратегій у матричних іграх за кінцеве число повторювань
гри.
, що теоретично можливо лише при нескінченному повторюванні
цієї гри. Натомість на практиці, коли моделлю реальної ситуації є матрична гра,
кількість повторювань гри завжди обмежена. Тому виникає проблема реалізації
оптимальних змішаних стратегій у матричних іграх за кінцеве число повторювань
гри.
Припустимо, що число повторювань гри ![]() з матрицею (1) відоме
і
з матрицею (1) відоме
і ![]() ,
, ![]() . Обом гравцям необхідно знати свою тактику перебору чистих
стратегій, яка б забезпечила вибір кожної з них
. Обом гравцям необхідно знати свою тактику перебору чистих
стратегій, яка б забезпечила вибір кожної з них ![]() раз і, таким чином, середній
виграш або програш (5). Нехай кожен з гравців дотримуватиметься наступної
тактики перебору чистих стратегій: спочатку вибирається
раз і, таким чином, середній
виграш або програш (5). Нехай кожен з гравців дотримуватиметься наступної
тактики перебору чистих стратегій: спочатку вибирається ![]() раз поспіль одна з
чистих стратегій, а потім — вибирається
раз поспіль одна з
чистих стратегій, а потім — вибирається ![]() раз інша. Тоді за
такої тактики перебору чистих стратегій існує чотири варіанти перебігу
раз інша. Тоді за
такої тактики перебору чистих стратегій існує чотири варіанти перебігу ![]() партій гри, де перший
гравець спочатку вибирає
партій гри, де перший
гравець спочатку вибирає ![]() раз поспіль
раз поспіль ![]() -ту чисту стратегію, а другий — вибирає
-ту чисту стратегію, а другий — вибирає ![]() -ту чисту стратегію,
-ту чисту стратегію, ![]() ,
, ![]() . Позначимо відповідний виграш першого гравця при
. Позначимо відповідний виграш першого гравця при ![]() -му розігруванні через
-му розігруванні через ![]() ,
, ![]() . Тоді середній виграш першого гравця за усі
. Тоді середній виграш першого гравця за усі ![]() розігрувань для
кожного з зазначених чотирьох варіантів відповідно дорівнює:
розігрувань для
кожного з зазначених чотирьох варіантів відповідно дорівнює:
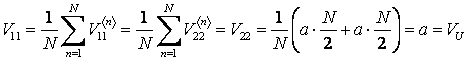 , (6)
, (6)
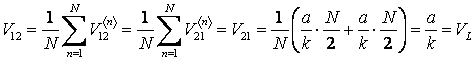 . (7)
. (7)
Вважаючи усі чотири варіанти перебігу ![]() розігрувань
рівноімовірними, можемо обчислити очікуваний виграш першого гравця (програш
другого гравця):
розігрувань
рівноімовірними, можемо обчислити очікуваний виграш першого гравця (програш
другого гравця):
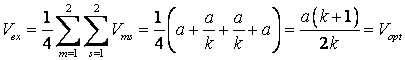 . (8)
. (8)
Отже, вищезгадана тактика перебору чистих стратегій для реалізації
оптимальних змішаних стратегій у грі з матрицею виграшів (1) за кінцеве число
повторювань гри ![]() є прийнятною для
кожного з гравців.
є прийнятною для
кожного з гравців.
Але розглянемо ![]() -гру з несиметричною матрицею виграшів виду
-гру з несиметричною матрицею виграшів виду
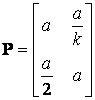 , (9)
, (9)
де ![]() ,
, ![]() і
і ![]() . Маємо
. Маємо ![]() при
при ![]() ,
, ![]() при
при ![]() , а
, а ![]() . Таким чином,
. Таким чином, ![]() і
і ![]() ,
, ![]() , де
, де
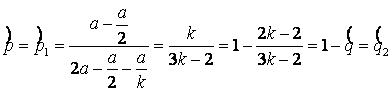 , (10)
, (10)
 . (11)
. (11)
Тут подібна тактика, яка полягає у виборі кожним з гравців спочатку однієї
з двох своїх чистих стратегій ![]() та
та ![]() раз поспіль відповідно,
раз поспіль відповідно,
![]() ,
, ![]() , не може бути застосована, оскільки
, не може бути застосована, оскільки ![]() не завжди націло
ділиться на
не завжди націло
ділиться на ![]() . Тобто, якщо
. Тобто, якщо ![]() та
та ![]() не є цілими числами,
то необхідно шукати іншу тактику перебору чистих стратегій, яка б забезпечила
подібну до (8) тотожність. Це є предметом подальших досліджень у цьому
напрямку.
не є цілими числами,
то необхідно шукати іншу тактику перебору чистих стратегій, яка б забезпечила
подібну до (8) тотожність. Це є предметом подальших досліджень у цьому
напрямку.