Бурцев Игорь Олегович

Иркутский национальный исследовательский технический университет, Россия

Точная формула приращения функционала в дискретных задачах. Достаточные условия оптимальности

Эффективным средством исследования задач оптимального управления является принцип максимума Понтрягина [1], представляющий собой необходимое условие оптимальности в таких задачах. Принцип максимума, открытый коллективом российских математиков во главе с академиком Л. С. Понтрягиным, представляет собой одно из крупных достижений современной математики и является краеугольным камнем современной математической теории оптимального управления.

Поскольку задачи дискретного оптимального управления фактически являются задачами математического программирования специальной структуры, то для них в общем случае не имеет места аналог принципа максимума Понтрягина – фундаментальное необходимое условие оптимальности в непрерывных задачах оптимального управления. Тем не менее, значительные усилия математиков были посвящены выделению классов задач дискретного оптимального управления, в которых принцип максимума справедлив, возможно в несколько ослабленной форме «квазимаксимума» [2; 3; 4].

Полученные в [5] достаточные условия оптимальности для непрерывных задач оптимизации основаны на точной формуле приращения функционала с использованием ключевой конструкции позиционного ПМ – возмущения котраектории градиентом целевой функции . В данной работе приводится формулировка точной формулы приращения функционала, а также достаточные условия оптимальности для дискретных задач оптимизации.

Здесь и далее будем пользоваться сокращенным обозначением, вынося переменную под знак индекса.

Рассмотрим задачу оптимального управления ()

где – последовательности , т.е. фазовая и управляющая траектории. Множества компактны , функции гладкие по при фиксированных , целевая функция гладкая.

Задача () рассматривается на множестве допустимых пар последовательностей . Через обозначается допустимая пара последовательностей, исследуемая на оптимальность.

Предположим, что в задаче () выполнено условие выпуклости: при всех если и то найдется такое что выполняется условие

Введем в рассмотрение функцию Понтрягина

и сопряженную систему

– котраектория процесса .

Теорема. Если пара оптимальна в задаче (), тогда функция Понтрягина достигает максимального значения на этом процессе, т.е.

где траектория находится из фазовой системы, а котраектория – из сопряженной.

Определим более жесткое условие выпуклости для задачи :

Пусть далее пара – фиксирована, – произвольные допустимые пары последовательностей, – любая последовательность со свойством

Рассмотрим выражение

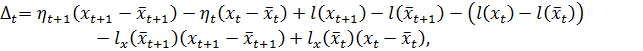
Тогда легко убедиться, что

С другой стороны, если ввести функцию Понтрягина

(1)

и обозначение

(2)

то выражение после раздельной группировки слагаемых с и можно представить в следующем виде:

(3)

Таким образом, мы получаем точную формулу приращения функционала

Лемма. Пусть в задаче функция непрерывно дифференцируема (отображения и множества произвольны). Тогда справедлива формула приращения (3), в которой функция определена равенствами (1), (2).

Эта лемма (т.е. фактически формула приращения (3)) служит источником (основой) для получения необходимых и достаточных условий оптимальности допустимого процесса .

Следующее условие достаточно для оптимальности процесса : пара векторов является решением задачи

при подходящем выборе траектории .

Рассмотрим это условие подробно, считая функции гладкими. Мы имеем

Для выполнения условия необходимо, чтобы вектор был решением задачи

Это дает равенство

Приводя подобные, получаем сопряженное уравнение

Таким образом, неопределенность в выборе исчезла.

Теперь рассмотрим необходимое условие для выполнения , т.е. фактически , ибо уже определена. А именно: должен быть решением задачи

(4)

Это дает следующее условие минимума:

(5)

или, в другой форме,

Условие минимума (4) или (5) не совпадает с условием минимума в ПМ терминальной задачи . Но структура функции под знаком минимума совпадает с функцией Понтрягина дискретной задачи , в которой терминальный функционал заменен на суммарный

При этом траектория – это в точности котраектория задачи , эквивалентной .

Действительно, если ввести вспомогательную фазу

то

При этом в расширенной системе для с критерием котраекторией будет , так что функция Понтрягина для задачи совпадает с

Условие (4) или (5) – это условие из ПМ задачи . Но этот ПМ имеет место только при выполнении условий выпуклости (В1), (В2).

Таким образом, в задачах класса , в которых выполнены условия выпуклости (В1), (В2), условие минимума (4) или (5) оказывается и необходимым.

(6)

Рассмотрим вспомогательную нелинейную (по ) функцию

Тогда удовлетворяет граничному условию

(7)

(8)

(т.к. ), а функция может быть записана в виде

Если сравнить (7), (8) с конструкциями Кротова, то можно заметить, что при вида (6) функция совпадает с традиционной для достаточных условий функцией , а другая кротовская конструкция в силу граничного условия (7).

Отсюда следует, что приведенные достаточные условия – это вариант достаточных условий Кротова с конкретно заданной вспомогательной (кротовской) функцией (6). Кроме того, отсюда следует и легко проверяемое равенство

Оно объясняет происхождение формулы приращения (3), а также дает другой способ обоснования достаточных условий оптимальности.

В результате данной работы была приведена формулировка точной формулы приращения функционала, а также были получены достаточные условия оптимальности для дискретных задач оптимизации.

Литература:

1. Понтрягин Л. С, Болтянский В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Математическая теория оптимальных процессов. — М.: Наука, 1976.

2. Пропой А. И. Элементы теории оптимальных дискретных процессов.– М.: Наука. Гл. ред. физ.-мат. лит., 1973.

3. Иоффе А. Д., Тихомиров В. М. Теория Экстремальных задач.– М.: Наука, 1974.

4. Мордухович Б. Ш. Методы аппроксимаций в задачах оптимизации и управления.– М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 360 с.

5. Дыхта В. А. Позиционные усиления принципа максимума и достаточные условия оптимальности. // Тр. ИММ УрО РАН. – 2015. –Т. 21, № 2. – С.73-86.