0EmpovD

УДК 517.9

И. А. Долгарев

ПОЛУЧЕНИЕ ПОВЕРХНОСТИ

3-МЕРНОГО ГАЛИЛЕЕВА ПРОСТРАНСТВА С РАСТРАНОМ

ПО КОЭФФИЦИЕНТАМ ЕЕ КВАДРАТИЧНЫХ ФОРМ.

В евклидовой дифференциальной геометрии регулярная поверхность обычно задается векторной функцией двух параметров, функция определена на некоторой области из , где поле действительных чисел. Для поверхности выписываются первая и вторая квадратичные формы + и . Коэффициенты формы выражаются через производные первого порядка функции , коэффициенты формы выражаются через производные второго порядка функции и вектор нормали поверхности. На основе первой квадратичной формы для поверхности вводятся метрические понятия, на основе второй квадратичной формы вводится кривизна поверхности. Квадратичные формы поверхности полностью характеризуют поверхность. Согласно теореме Бонне, коэффициенты квадратичных форм поверхности евклидова пространства определяют и саму поверхность с точностью до положения в пространстве, см., например, [1]. В работе [2] установлено, что и в пространстве Галилея поверхность определяется коэффициентами ее первой и второй квадратичных форм.

Обобщением пространства Галилея являются одулярные галилеевы пространства. При этом векторное пространство пространства Галилея заменяется одулем Ли . Некоммутативный действительный одуль Ли получается в результате определения внешней операции умножения элементов группы Ли на действительные числа. Поверхность в 3-х мерном галилеевом пространстве задается на основе некоммутативного векторного поля евклидовой плоскости. Свойства векторных полей и поверхности одулярных галилеевых пространств взаимосвязаны. Поэтому интересно изучить поверхности одулярных галилеевых пространств. В общем виде структура одуля введена Л.В. Сабининым в [3].

Ниже рассматривается одно из одулярных галилеевых пространств, так называемое ЕМ- пространство, одуль Ли которого – растран состоит из параллельных переносов и гомотетий аффинного пространства. Устанавливается, что поверхность этого пространства определяется с точностью до положения в пространстве коэффициентами первой и второй квадратичных форм. Результаты получены интегрированием дифференциальных уравнений в частных производных. Эти уравнения возникают в процессе исследования свойств поверхностей ЕМ-пространства, [4]. Используется метод последовательного интегрирования уравнений, развиваемый ниже и заложенный в [2]. Во второй половине работы найдена поверхность ЕМ-пространства, коэффициенты квадратичных форм которых постоянны.

Решению основной задачи о получении поверхности предшествует вводный параграф 1 с основными определениями и результатами для поверхностей ЕМ-пространства.

1. Растран и ЕМ-пространство.

1.1. Одули Ли размерности 3.

Действительным одулем Ли является структура, полученная на действительной группе Ли в результате определения внешней операции умножения элементов группы Ли на действительные числа. Внешние операции на 2- и 3-мерных одулях Ли введены в [4]. Групповая операция записывается аддитивно.

Имеется пять видов 3-мерных разрешимых действительных одулей Ли. Среди них линейное пространство (единственный коммутативный одуль Ли) и однородный растран. На многообразии однородный растран задается следующими операциями (;):

, , .

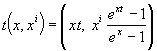Элементы растрана называются растами и обозначаются ; – нулевой раст, для всякого раста : . Пусть , , . Имеется разложение

.

Упорядоченное множество является ортонормированным базисом растрана . Расты составляют подрастран, являющийся 1-мерным линейным пространством ; расты составляют 2-мерное линейное пространство . Растран есть полупрямая сумма линейных пространств = L²┤L¹, подрастран L² является инвариантным в растране .

1.2. Галилеева норма на растране.

Галилеевой нормой ||w|| раста w=(x, x¹, x²) называется

, если x ≠ 0;

, если x = 0.

Линейные пространства и превращаются в евклидовы векторные пространства соответственно и , нормированный растран является полупрямой суммой евклидовых пространств =┤. Составляющая этой суммы – времениподобна, составляющая – пространственноподобна.

Расты (0,x¹,x²) называются евклидовыми, это векторы евклидова пространства , растры (0,x¹,x²), x≠0, называются галилеевыми. Всякий галилеев раст перпендикулярен всякому евклидову расту. [4].

1.3. Дифференцирование одулярных функций.

Отображение R® называется растранной функцией одного параметра. Обычно рассматривается интервал I в R или R. Значению tÎI соответствует раст r(t)=(x(t), x¹(t), x²(t)). Растранная функция r(t) представляет собой упорядоченную совокупность (x(t), x¹(t), x²(t)) трех действительных функций действительного параметра. Рассматриваем функции класса C ³, т.е. каждая из действительных функций x(t), x¹(t), x²(t) обладает производными до третьего порядка включительно.

Производная функция = одулярной функции r(t) определяется равенством

.

Получена следующая формула дифференцирования растранных функций, [4]:

.

Свойства дифференцирования векторных функций на растранные функции не распространяются. В частности, , производная суммы растранных функций не равна сумме производных этих функций.

Производные второго порядка растранных функций есть производные от производных первого порядка.

Отображение называется растранной функцией двух параметров. Рассматривается некоторая односвязная область или . Паре соответствует раст . Частные производные , отыскиваются как производные функций одного параметра (либо , либо ). Для растрана:

смешанная производная второго порядка растранной функции зависит от порядка дифференцирования.

1.4. Определение ВО-пространств и ЕМ-пространств.

Пусть W непустое множество, его элементы называются точками их обозначение: A, B,¼,M,¼, и W одуль Ли. Задано отображение пар точек (A, B) в одуль Ли W, т.е. всякой паре (A, B) точек соответствует единственный одуляр w, пишем: AB=w ; выполняются аксиомы Г. Вейля

(в.1) для всякой точки А и всякого одуляра w существует единственная точка В,

что AB=w;

(в.2) для любых трех точек А, В, С, если AB=w, AC=c, то AC=w+c.

Множество W называется вейлевским одулярным пространством; кратко ВО-пространством; одуль Ли W называется одулем ВО-пространства W. Одуляры из W называются одулярами ВО-пространства W.

ВО-пространство является частным случаем одулярных пространств Л.В. Сабинина, [3]. Если W = , то W аффинное пространство. Размерность одуля Ли W называется размерностью ВО-пространства W. Далее рассматриваются 3-мерные ВО-пространство с растраном. ВО-пространство с нормированным однородным растраном называется ЕМ-пространством и обозначается M³.

Пусть точка ЕМ-пространства M³, Б = (a, b, g) базис растрана . Множество B = (0, a, b, g) называется репером ЕМ-пространства. Это ортонормированный репер. Координатами точки M в репере B называются координаты раста OM в базисе Б. Если ОМ = (x, y, z), то и M = (x, y, z).

Для точек A = (a,a¹,a²) и B = (b,b¹,b²) имеем AB = (b-a, b¹-a¹e^b-a, b²-a²e^b-a). Расстоянием |AB| между точками A и B в ЕМ-пространстве равно норме раста AB. Согласно п. 1.2,

, если b ≠ a;

, если b = a.

ЕМ-пространство является одулярным галилеевым пространством.

1.5. Поверхности ЕМ-пространства.

В ЕМ-пространстве рассматриваем регулярные поверхности класса

= ,

Поверхность задается растранной функцией двух параметров. В ЕМ-пространстве содержатся поверхности, имеющие евклидовы касательные плоскости, и поверхности, имеющие неевклидовы касательные плоскости (т.е. ЕМ-плоскости). Поверхности с евклидовыми касательными плоскостями могут быть изучены средствами евклидовой геометрии, поэтому в геометрии ЕМ-пространства интересны оставшиеся поверхности. Ввиду того, что рассматриваются поверхности класса , поверхности интересующего нас вида описываются растранными функциями

= , . (1)

Такая параметризация поверхности называется естественной.

В репере = ЕМ-пространства имеем разложение

= + , (2)

где = векторная функция евклидовой плоскости = ЕМ-пространства, [4]. Это также векторное поле евклидовой плоскости, евклидова проекция поверхности на плоскость . Слагаемое есть времениподобная составляющая поверхности, параметр – время, – пространственноподобная составляющая.

Для поверхности (1) u – линии являются кривыми евклидовой плоскости, остальные линии на поверхности записываются как функции параметра t. Линии на поверхности

= ,

имеют единичный галилеев касательный раст , t – естественный параметр кривой.

На основании формул дифференцирования растранных функций, [4], имеем следующие частные производные первого порядка функции :

= = (x_u,y_u), = = (1, (e-1)(x_u-x), (e-1)(y_u-y));

Производные второго порядка одулярной функции таковы:

= , = , ; (3)

1.6. Деривационные формулы поверхностей ЕМ-пространства.

В соответствии с [4] имеем следующие формулы. Первая квадратичная форма поверхности r(u,t) есть

или , (4)

Вторая квадратичная форма поверхности:

(5)

ее коэффициенты

, , ; (6)

единичный вектор нормали поверхности равен

, . (7)

Как евклидов раст, вектор перпендикулярен всякой линии на поверхности, проходящей через рассматриваемую точку поверхности. Нормальная кривизна поверхности вычисляется по формуле

,

-направление на поверхности. Полная, т.е. гауссова кривизна равна

. (8)

Деривационные формулы поверхности, используемые ниже:

,

,

, (9)

.

1.6. Основные уравнения теории поверхностей ЕМ-пространства.

К основным уравнениям теории поверхностей относится формула Гаусса и две формулы Петерсона-Кодацци. Имеем формулу Гаусса [4]:

(10)

и две формулы Петерсона-Кодацци

, . (11)

На основании приведенных результатов имеем следующее свойство: полная кривизна поверхности ЕМ-пространства относится к внутренней геометрии поверхности.

2. Опредление поверхности ЕМ-пространства М³

по коэффициентам первой и второй квадратичных форм

2.1. Постановка задачи.

На односвязной области D евклидовой плоскости E² ЕМ- пространства М³ заданы функции:

E = E(u,t) ³ 0, A = A(u,t), B = B(u,t), C = C(u,t) (12)

Класса C², удовлетворяющие уравнениям (10) и (11). Требуется найти векторную функцию класса C³

,

определенную на той же области D, функция является пространственноподобной составляющей поверхности r(u,t) (2) ЕМ-пространства М³ ; через производные растранной функции r(u,t) выражаются заданные функции (12), см. соотношения (4) и (6). Вектор (7) – единичный вектор нормали поверхности r(u,t). Первая квадратичная форма поверхности r(u,t) есть (4), вторая квадратичная форма поверхности есть (5). Т.е. поверхность r(u,t) пространства М³ нужно задать, зная коэффициенты ее первой и второй квадратичных форм. Производные второго порядка растранной функции r(u,t) удовлетворяют деривационным формулам (9).

Для однозначного определения поверхности r(u,t) заданы начальные условия:

, , , , (13)

где , , , заданные векторы, и не коллинеарны.

По параметру u растранная функция r(u,t) дифференцируется как векторная, см. п.1.5. Для векторной функции выполняется свойство

(р) компоненты x(u,t), y(u,t) функции удовлетворяют обычным условиям C ³ -функций: смешанные производные этих функций не зависят от порядка дифференцирования.

Сформулированная задача сводится к доказательству теоремы о поверхностях ЕМ-пространства, аналогичной теореме Бонне в евклидовой геометрии, [1]. Ранее такая теорема доказана для пространства Галилея [2]. Доказывается следующее утверждение.

Основная теорема.

Если на односвязной области D евклидовой плоскости ЕМ-пространства М³ заданы функции (12) класса C³ , для которых выполняются условия (10), (11), то на области D определяется функция , удовлетворяющая соотношениям (9). В ЕМ-пространстве М³ существует единственная, удовлетворяющая условиям (13), поверхность , первой и второй квадратичным формам с коэффициентами (12).

Доказательство теоремы содержится в пп. 2.3 – 2.6.

2.2. Метод последовательного интегрирования.

В [2] для отыскания поверхности пространства Галилея по коэффициентам ее квадратичных форм отыскивались функции двух переменных по их частным производным, т.е. интегрировались уравнения в частных производных. Был использован метод последовательного интегрирования уравнений, благодаря которому решались только уравнения первого порядка. Согласно специфике пространства Галилея, решались только уравнения с полным дифференциалом. Сначала по частным производным , , найдены функции и . Условия интегрируемости уравнений обеспечены деривационными формулами поверхности и уравнениями Петерсона-Кодацци. Используется так же зависимость между первой квадратичной формой поверхности и ее нормалью для 3-мерного галилеева пространства. По условию решаемой задачи, частные производные отыскиваемой функции не даны, но даны функции, выражаемые через частные производные неизвестной функции – скалярные функции E(u,t), A(u,t), B(u,t), C(u,t), а находились векторные функции , . Далее решаются стандартные задачи нахождения функции по функциям и .

И в уравнениях с полным дифференциалом для компонент функций , задействованы не сами функции , , , а некоторые другие функции, полученные на их основе. Т.е. к уравнениям второго порядка с частными производными мы не приходим на втором этапе.

Ниже тем же методом последовательного интегрирования уравнений в частных производных отыскиваются поверхности ЕМ-пространства М³ по коэффициентам их квадратичных форм. Функция находится как и в пространстве Галилея. На первом этапе этого метода для функции уравнений с полным дифференциалом не получается. Это зависит от специфики ЕМ-пространства. Сначала отыскиваются решения некоторых вспомогательных уравнений в частных производных, а затем на основании независимости смешанных производных евклидовых векторных функций от порядка дифференцирования отыскивается функция .

Далее следует стандартный второй этап решения задачи.

Существенно используется условие (p) из п.2.1: по найденным функциям и отыскиваются функция , т.е. функция отыскивается по ее частным производным и .

2.3. Отыскание функции .

Ищем функцию в виде

, , .

Все точки (u,t)ÎD. Для функции выполняется (4). Обозначим

, (14)

На основе равенства

введем обозначения

, , (15)

функцию w = w(u,t) предстоит найти. Воспользуемся функцией (7). По (15),

=, (16)

вектор является единичным вектором нормали поверхности r(u,t), выполняется .

В новых обозначениях первое и второе равенство из (6) принимает вид

(17)

(18)

Дифференцируем равенства (15):

,

По уравнению (17) находим

, ,

По уравнению (18) имеем

.

Для функции w = w(u,t) выполняется условие w_ut = w_tu. Действительно,

, .

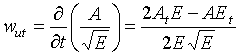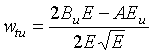Из первой формулы Петерсона-Кадацци (11) имеем

,

что и означает выполнимость условия w_ut = w_tu,

.

Следовательно, приходим к уравнению в полным дифференциалом

.

Решение этого уравнения есть функция w = w(u,t).

Теперь, согласно (15), становятся известными функции:

,

и векторная функция

.

Имеем

.

Начальные условия, см (13), , или в компонентах ,

, определяет единственное значение функции и единственное значение функции в точке (u₀,t₀) области D.

2.4. Отыскание функции .

Воспользуемся функциями , , см. (3) и деривационными формулами (9) , . Для производной r_tt имеем векторное уравнение

.

Перепишем это уравнение для компонент его векторов

, , (19)

здесь данная функция, см (12), функция найдена выше, см. (16). На основании двух рассматриваемых равенств для производной имеем векторное уравнение:

или

оно равносильно двум уравнениям для компонент содержавшихся в нем независимых векторных функций:

, , (20)

здесь , данные функции, см. (12), функции , , уже найдены в предыдущем п. 2.3. Неизвестная функция удовлетворяет первому из уравнений (19) и первому из уравнений (20). Функция удовлетворяет вторым уравнениям (19) и (20). Решая первое из уравнений (19), находим функцию , зависящую от некоторой неизвестной функции , которую находим, воспользовавшись первым уравнением (20). Аналогично получаем функцию . Здесь используется условие (p) из п. 2.1.

Правую часть первого из уравнений (19) обозначим . Решаем уравнение

,

обозначив

.

Приходим к линейному уравнению

.

Это обыкновенное дифференциальное уравнение для функций от одной переменной и параметра . Производим подстановку

, , , .

В полученном в результате уравнении

отыскиваем функцию как решение уравнения , где , (это функция аргумента , зависящая от параметра ). Имеем

.

Приходим к уравнению

.

Откуда

.

Так как , то имеем выражение функции = через неизвестную функцию :

.

Функцию найдем, прибегнув к первому из уравнений (20), обозначив его правую часть :

.

Находим, дифференцируя по параметру :

.

Обозначим . Таким образом

.

Отсюда получаем

.

Следовательно,

Функция имеет своим аргументом , поэтому произвольная постоянная, дифференцирование по с последующим интегрированием функции приводит к , т.е.

.

Теперь функция имеет вид:

;

таким образом,

.

Подставим сюда значение 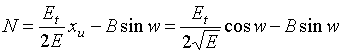, см. (15) и окончательно получим

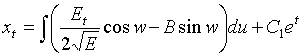. (21)

Аналогично находится функция :

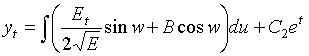. (22)

Тем самым, найдена функция . По начальному условию , см. (13), определяется единственная функция для которой , .

2.5. Отыскание функции .

Функции и , полученные в пп. 2.3 и 2.4, являются частными производными функции , согласно условию (р), приводит к двум уравнениям с полным дифференциалом:

, .

Их решения являются функция . Начальные условие , см. (13), дает единственную функцию , определяемую функциями (4), (6).

2.6. Поверхность с заданными коэффициентами квадратичных форм.

Согласно п. 2.5, условия основной теоремы п. 2.1 обеспечивают существование единственной векторной функции ; тем самым существует единственная поверхность = , , ЕМ-пространства , определяемой функциями (12). В п. 2.3 по условиям основной теоремы найдена функция . Т.к. = и , то найденная поверхность имеет первую квадратичную форму (4) или . Также в п.2.3 найден вектор – единичный вектор нормали поверхности . По формулам (6) получаем, что поверхность имеет вторую квадратичную форму (5) с заданными коэффициентами . Действительно, например по первому равенству в (9): . Следовательно, основная теорема об определяемости поверхности ЕМ-пространства функциями, задающими квадратичные формы поверхности, сформулированная в п. 2.1, доказана полностью. В точке определяется единственная поверхность, имеющая касательную плоскость, натянутую на векторы и .

3. Поверхность ЕМ-пространства,

коэффициенты квадратичной формы которой постоянны.

3.1. Теорема для поверхности,

имеющей постоянные коэффициенты квадратичных форм.

Согласно основной теореме, п. 2.1., функции (12) и начальные условия (13) однозначно определяют поверхность ЕМ-пространства М³. Найдем какого вида поверхность получается в случае, если коэффициенты квадратичных форм постоянны. Эти поверхности описываются следующей теоремой.

Теорема. Если коэффициенты первой и второй квадратичных форм поверхности ЕМ-пространства М³ постоянны, то ненулевыми могут быть только два из них: и , два других равны нулю:. Поверхность определяется растранной функцией

= ,

где . Это цилиндрическая поверхность; ее образующие есть линии – пространственноподобные прямые; направляющие есть линии – плоские линии постоянной кривизны . Полная кривизна поверхности равна нулю. Нормальная кривизна поверхности постоянна и равна .

Доказательство теоремы содержится в пп. 3.2 - 3.4.

3.2. Производная по пространственноподобному параметру.

По формуле Гаусса (10), формула полной кривизны K поверхности содержит производные E_t и E_tt. Так как коэффициент E постоянен, то по формуле (10),

K = 0. (23)

Согласно равенству (4) и обозначениям , в п. 2.3, с учетом , получаем:

, .

В п. 2.3 так же получено

, .

Решая уравнение с полным дифференциалом

(24)

имеем линейную функцию w:

, (25)

где C₀ постоянное слагаемое. Таким образом . Модуль векторной функции постоянен: . Единичный вектор нормали поверхности есть

.

3.3. Пространственнподобная составляющая.

Согласно п. 3.2, для функции = имеем

, .

По функциям и будем находить функции и . Интегрирование по параметру на основе (24) дает:

, .

Как всегда, при интегрировании по одному из параметров функции , постоянное слагаемое первообразной функции может зависеть от другого параметра. Функции b₁(t) и b₂(t) найдем из значений производных функций и по параметру и начальных условий. Имеем:

, ;

, .

По (19), , поэтому

. (26)

Из (23) и , следует

.

Поэтому (27) превращается в: , или

.

Функция зависит только от одного параметра , следовательно, либо и зависит только от параметра , либо и . Равенство означает, что функции , есть постоянные величины, что невозможно (поверхности не существует). Значит, поверхность существует только в случае, если функция параметра :

, .

Из последнего равенства и (23) следует

,

поэтому

.

Выполняется

Теорема. Если поверхность ЕМ-пространства имеет квадратичные формы, коэффициенты которых постоянны, то для второй квадратичной формы (5) поверхности: .

Поэтому при интегрировании функций , имеем

= , . (27)

В этом случае

, , , ,

и по (19) приходим к уравнению

с постоянными коэффициентами и постоянной правой частью. Решением этого уравнения является

= , – произвольные постоянные.

Таким образом, мы получили, см. (27):

. (28)

Аналогично,

. (29)

Тем самым, определена пространственноподобная составляющая = = поверхности r(u,t). Условия (13) определяют единственную, проходящую через точку (u₀,t₀).

3.4. Поверхность ЕМ-пространства.

Согласно п. 1.5, поверхность ЕМ-пространства описывается растранной функцией (2) . Составляющая найдена в предыдущем п. 3.3.

В движениях ЕМ-пространства один ортонормированный репер можно заменить другим ортонормированным репером. Формулы замены координат таковы:

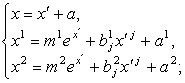
см [4, с.136]. Поэтому существует репер ЕМ-пространства, в котором в задании поверхности (28), (29): , , т.е. в подходящем репере найденая поверхность описывается растранной функцией:

= ,, ). (30)

Для этой поверхности:

= и ; и ;

и ;

= , ; = ;

с учетом , .

Найденная поверхность (30) имеет линии

= ,, ),

являющиеся прямыми евклидовых плоскостей, т.е. пространственноподобные прямые, и линии

= ,, )

являющиеся линиями постоянной кривизны. Кривизна линии ЕМ-пространства вычисляется по формуле , [4, c.139], линии заданы в естественной параметризации. Имеем . Кручение линий равно нулю и линии плоские. Это цилиндрическая поверхность с евклидовыми образующими, направляющие которой есть линии постоянной кривизны ЕМ-плоскостей ЕМ- пространства. Полная кривизна поверхности, как уже отмечено выше, равна нулю. Нормальная кривизна поверхности равна

,

см. п. 1.6, это поверхность постоянной нормальной кривизны.

Теорема п. 3.1. полностью доказана.

Выше доказана теорема Бонне для поверхностей ЕМ-пространства и найдены поверхности ЕМ-пространства, имеющие постоянные коэффициенты в первой и второй квадратичных формах.

Литература.

1. П о з н я к Э. Г., Ш и к и н Е. В. Дифференциальная геометрия. – М.: Изд-во МГУ, 1990. – 384с.

2. Д о л г а р е в И. А. Задание поверхности галилеева пространства-времени ее квадратичными формами.//

3. С а б и н и н Л. В. Одули как новый подход к геометрии со связностью// ДАН СССР. 1977. № 5.- С. 800 – 803.

4. Д о л г а р е в А. И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

Долгарев Иван Артурович,

Аспирант кафедры МММ Пензенского университета.

E-mail: delivar@yandex.ru