Математика/5. Математическое
моделирование
Махамбетова Г.И.
Костанайский государственный университет им.А.Байтурсынов, Казахстан
ОБРАТНАЯ
ЗАДАЧА КОНДУКТИВНОГО РАСПРОСТРАНЕНИЯ ТЕПЛА В ОДНОРОДНОЙ СРЕДЕ
Недостаток сведений о физических и физико-химических причинах,
вызывающих миграцию влаги при промерзании, а также процессах, которые ее
сопровождают, не позволяет пока получить надежные методы определения
коэффициента теплопроводности, влагопроводности и т.д. в промерзающих почвах и
тонкодисперсных горных породах. В серии работ /1-5/ были разработаны методика
решения распространения тепла и влаги в многослойной области. Известно что, не
зная решения прямой задачи, нельзя взяться за решение обратной задачи. Следует
отметить, что самым сложным вопросом является определение коэффициента
теплопроводности, в фазовой зоне. В этой работе приводится приближенный метод,
с помощью которой определяется коэффициента теплопроводности грунта.
1. Постановка задачи ![]() , (1)
, (1)
![]() ,
, ![]() , (2)
, (2) ![]() ,
, ![]() , (3)
, (3)
Требуется определить коэффициент теплопроводности ![]() .
.
Численное
решение задачи (1)-(3) будем искать из минимума функционала: 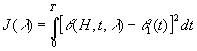 .
.
Зададим
начальное приближение ![]() . Следующие приближенное решение
. Следующие приближенное решение ![]() будем вычислять
методом простых итераций:
будем вычислять
методом простых итераций:
![]() ,
,
здесь ![]() - достаточно малое число,
- достаточно малое число, ![]() - градиент
функционала
- градиент
функционала ![]() . Коэффициенты
. Коэффициенты ![]() и
и ![]() удовлетворяют системе
(1) – (3). Обозначим
удовлетворяют системе
(1) – (3). Обозначим
![]() ,
, ![]() .
.
Тогда для перемещения получаем задачу:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
2. Градиент
функционала
Умножим
(1) на ![]() и проинтегрируем по z и t
в области
и проинтегрируем по z и t
в области ![]() . После несложных преобразований получим сопряженную задачу:
. После несложных преобразований получим сопряженную задачу: ![]()
![]() ,
, ![]()
![]()
Вычислим приращение функционала
![]()
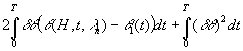 .
.
Используя уравнение, начально-краевые
условия сопряженной задачи выводим, что
![]()
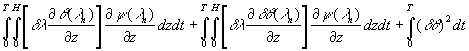 .
.
Две последние слагаемые в правой части
последнего равенства имеют второй порядок малости. Тогда получаем следующий
градиент функционала:
![]() .
.
3. Алгоритм
решения задачи
1) Пусть приближение ![]() известно
известно
2) Решается прямая задача
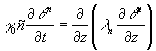 , (4)
, (4)
![]() , (5)
, (5)
![]() ,
, ![]() (6)
(6)
и определяется ![]() и
и ![]() .
.
3) Решается сопряженная задача
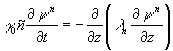 (7)
(7)
![]() ,
, ![]() (8)
(8)
![]() (9)
(9)
4) Вычисляется градиент функционала
![]() .
.
5) Следующее приближение коэффициента теплопроводности
определяется по формуле: ![]() ,
, ![]()
4. Априорные
оценки прямой задачи
Теорема 1. Для решение задачи (4)-(6) справедливо
оценка
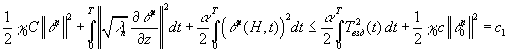 . (10)
. (10) ![]()
Теорема 2. Для решение задачи (7)-(9) справедливо
оценка
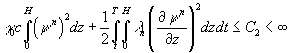 , (11)
, (11)
На основе (10) и (11) получаем, что
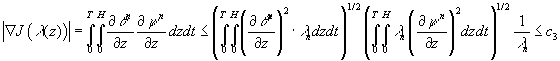 .
.
Теорема 3. Последовательность ![]() сходится к одному пределу и ограничено сверху и снизу
положительной константой.
сходится к одному пределу и ограничено сверху и снизу
положительной константой.
Теорема 4. Последовательность ![]() является монотонно
убывающей и ограничено сверху положительной константой.
является монотонно
убывающей и ограничено сверху положительной константой.
Литература:
1
Адамов А.А. Процессы
протаивания грунта // Доклады НАН РК. -2007. -№1. - С. 16-19.
2
Рысбайұлы Б.,
Адамов А.А. Исследование теплопроводности фазовой зоны в многослойном грунте // Вестник НАН РК. 2007. -№4. - С. 30-33.
3
Мартынов Г.А. Тепло - и
влагоперенос в промерзающих и оттаивающих грунтах. Основы геокрилогии
(мерзлотоведения). – М.: 1959, под. ред. Н.А. Цытович. гл. VI стр. 153-192.
4
Чудновский А.Ф. Теплобмен
в дисперсных средах. – М. Гостехиздат, 1954, 444 с