моделирование устойчивости газопылевых облаков в поле двойных звездных систем

 

  И.У. Махамбаева

 

Рассматривается фотогравитационная ограниченная  задача трех тел, в которой оба основных гравитирующих тела являются источниками излучения световой энергии.

Движение частицы  пренебреженно малой массы будем изучать в поле двух гравитирующих и одновременно излучающих тел  и , считаемых материальными точками, и,  обращающихся друг относительно  друга по кеплеровой орбите. Начало О прямоугольной системы координат  поместим в центр масс основных тел; ось Ox направим вдоль прямой, соединяющей основные тела, а ось Oz – перпендикулярно плоскости их орбитального движения в сторону, откуда вращение видно происходящих против хода часовой стрелки. При этом для удобства выберем следующие единицы измерения: сумму масс основных тел  и  примем за единицу массы, расстояние между ними – за единицу длины, отношение  T/2p - за единицу времени (где Т- период обращения основных тел).

Тогда движение частицы задается каноническими уравнениями

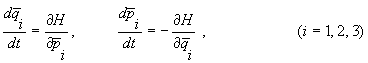                      (1)

где   суть декартовые координаты частицы  , - соответствующие канонические импульсы, а  - аналитическая функция Гамильтона относительно координат и импульсов, которая в нашем случае имеет вид

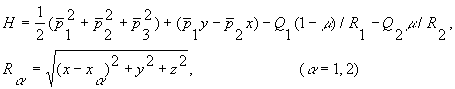   (2)

Здесь  и  - коэффициенты редукции масс основных тел, зависящие от интенсивности их излучения и парусности изучаемой частицы, характеризуемой отношением площади поперечного сечения к ее массе.

Известно, что дифференциальные уравнения (1) задачи не имеют общего решения.  Однако известны частные решения, отвечающие положениям относительного равновесия. Если классическая задача допускает пять точных  частных решений, то в фотогравитационной задаче существуют  трехпараметрические семейства девяти частных решений,  три из них (коллинеарные точки либрации) расположены на оси Ox, два (треугольные точки либрации)- в орбитальной плоскости, а четыре (компланарные точки либрации)– вне плоскости орбитального движения основных тел.

Исследуем устойчивость треугольных точек либрации в предположении, что орбита основных тел круговая, а тело Р бесконечно малой массы в начальный момент времени испытывает только те возмущения, не выводящие его из плоскости вращения основных тел  и .В уравнения (1) вводим возмущения по формулам

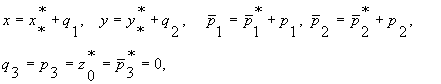        (3)

где   

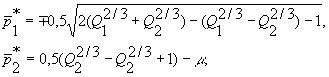                                (4)

и     раскладывая гамильтониан в ряд по степеням возмущений и  в окрестности рассматриваемой точки, принимаемой за начало координат, получим

                                                                     (5)

Здесь - однородные полиномы степени    относительно обобщенных координат  и импульсов     , так что

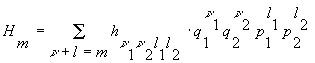                                    (6)

 

Тогда в выражении (5) формы  и  с учетом (3) и (4) примут следующий вид:

                  (7)

                                   (8)

 

                        (9)

где,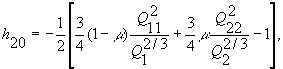    

Рассмотрим случай, когда  не является знакоопределенной функцией, а характеристическое уравнение системы не имеет корней с ненулевой вещественной частью (в противном случае тривиальное решение системы неустойчиво по Ляпунову).

Как видно из (4)  не является знакоопределенной функцией, и, следовательно,  из устойчивости линейной системы не следует устойчивость полной системы.

Полагая, что  в системе  отсутствуют резонансы 3-го и 4-го порядков, после применения преобразования Биркгофа и ограничиваясь разложением до четвертого порядка включительно, функцию Гамильтона можно записать в виде

                      (11)

Согласно теореме Арнольда-Мозера [6] при одновременном выполнении условий

                                                                         (12)

                                     (13)

где - целые числа,  удовлетворяющие условию  (- порядок резонанса), а - коэффициенты нормальной формы, зависящие от частот  и  линейной системы, для всех значений массового параметра m из области устойчивости линейной системы всюду сохраняется устойчивость по Ляпунову исходной системы (1). Исключение составляют множества точек, отвечающие резонансам 3-го и 4-го порядков, которые определяются  выражениями

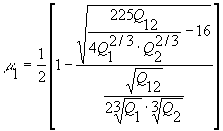                                                  (14)

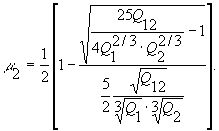                                                   (15)

При наличии в системе резонанса четвертого порядка      с помощью преобразования Биркгофа в исходном гамильтониане уничтожим члены третьей степени. Нормализованной при этом гамильтониан в полярных координатах примет следующий вид:

Здесь   .

Следует заметить, что если в классической задаче для конкретного значения m коэффициенты  и  принимают постоянные значения (что намного упрощается исследование задачи), то в фотогравитационной задаче  эти же коэффициенты не остаются постоянными и являются функциями  координат  x, y или  и , вследствие чего задача резко усложняется. Используя результаты А.П. Маркеева [7] получим, что при резонансе четвертого порядка , определяемого множеством точек из области устойчивости линейной системы, треугольные точки либрации при

а)  - устойчивы по Ляпунову,                                                   (18)

в)     -  неустойчивы,                                                                  (19)

где   .

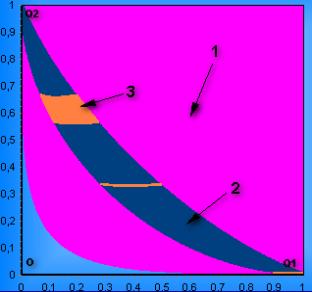
Численным исследованием было доказано, что для всевозможных значений параметров системы резонансные множества точек 3-го порядка в обобщенной фотогравитационной ограниченной задаче трех тел всегда неустойчивы. Построена область устойчивости треугольных точек для значения массового параметра μ=0,01 (рис.1).

 

 

Рис.1. Область устойчивости треугольных точек либрации при μ=0,01.

1 - область устойчивости в линейном приближении;2 – устойчивые множества точек  при резонанса  четвертого порядка;              3 - неустойчивые резонансные подмножества четвертого порядка.

 

 

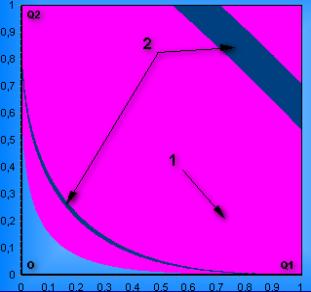
Рис. 2. Область устойчивости треугольных точек либрации при μ=0,01.

1 - область устойчивости в линейном приближении; 2 – множества точек, где .

 

 

Установлено, что в этом случае резонанс  3-го порядка не реализуется. Найдены  участки области, соответствующие резонансу , где выполняется неравенство, что свидетельствует об устойчивости по Ляпунову исследуемых точек либрации в плоском варианте задачи (в случае пространственной задачи имеет место устойчивость в 4-ом порядке); на других участках области, где неравенство меняет знак на обратной, имеет место неустойчивость исследуемых точек.

 Указаны области (рис.2), в которых  условие (13) не выполняется.

Таким образом,  на основе КАМ-теории доказана, что в области устойчивости в первом приближении треугольные точки в плоской задаче трех тел всюду устойчивы по Ляпунову за исключением множества точек, в которых реализуются резонансы , , и не выполняется условие  теоремы Арнольда-Мозера. Следовательно, вопрос об устойчивости треугольных точек либрации в плоской фотогравитационной задачи трех тел решен до конца.

 

Список   литературы

1.     Куницын.А.Л., Турешбаев.А.Т. Устойчивость треугольных точек

     либрации фотогравитационной задачи трех тел. // Письма в

     Астрон.журн.,  1985. Т.11. №2. C.145-148.

2.     Турешбаев А.Т.Об устойчивости компланарных точек либрации фотогравитационной задачи трех тел  // Письма в Астрон. журн. 1986. Т.12. №9. С.722-725.

3.     Лукьянов Л.Г. О семействе точек либрации в ограниченной фотогравитационной задаче трех тел // Астрон. журн. 1988. Т.65. №2. С.422-432.

4.     Kunitsin A.L., Tureshbaev A.T. On the collinear libzation points in the photo-gravitional three-body problem // Celest. Mech., 1985. V.35, Р.105-112.

5.     Пережогин А.А., Турешбаев А.Т. Об устойчивости треугольных точек либрации в фотогравитационной задаче трёх тел  // Астрон. журн. 1989, Т.66. С.859-865.

6.     Арнольд В.И. Математические методы классической механики. М.: Наука, 1974. 432 С.

7.     Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука. 1978. 312 С.