Технические науки/2. Механика

Гавеля Г.М.

Днепропетровский национальный университет им. О Гончара, Украина

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ВАРИАЦИОННЫХ ПОСТАНОВОК ОБРАТНЫХ ЗАДАЧ В ТЕОРИИ ОБОЛОЧЕК

При использовании идентификационного подхода для решения задач математической физики [1] одним из важнейших принимаемым фактором является выбор критерия идентификации. Искомые и наблюдаемые характеристики объекта исследования трактуются как элементы метрических пространств, а целевой функционал формулируется на основе невязки, соответствующей уклонению определенного по модели состояния от наблюдаемого в r-м из числа наблюдений в метрике пространства :

, ,

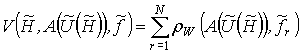где – вектор-функция решения обратной задачи теории оболочек, характеризующая физические и геометрические свойства, нагрузки, граничные условия; – метрика в функциональном пространстве ; – вектор перемещений; – множество возможных состояний оболочки.

В смысле устойчивости решения относительно малых возмущений входных данных задача (1) может оказаться некорректной. Так, наличие нескольких близких по некоторой норме решений при существенно различных параметрах состояния делает указанную задачу зависимой от вида функционала . Известно [2], что некорректность обратной задачи может быть преодолена за счет правильного выбора функциональных пространств и метрики на них и сужением области поиска решений путем задания некоторых априорных ограничений на их свойства, что обеспечивает регуляризацию некорректной задачи.

В данной работе предлагается идентифицировать параметры обратной задачи теории оболочек, учитывая особенности нелинейного напряженно-деформированного состояния (НДС), определяя физический смысл функций , и вводя специальное функциональное пространство и метрику в нем так, чтобы поиск решения обеспечивался на компакте. Выбор функционального пространства и метрики в нем связан со свойствами задачи, которая в рассматриваемом случае описывается функциями , полученными из решения прямых задач теории оболочек и характеризующими нелинейное НДС.

Предполагается, что каждой функции соответствует единственное решение . Тогда для устойчивости решений достаточно, чтобы было компактом [2]. Введение условия компактности в постановку задачи означает использование количественной информации об искомом решении. Таким образом, для определения регуляризированного приближения необходимо задать соответствующую метрику и компакт , который определяет область решений , причем компакт может быть задан ограничением на норму решений из числа допустимых. Кроме того, необходимо определить физический смысл вектор-функции , учитывая свойства решений прямой задачи теории тонких оболочек. Тогда задача определения неизвестных функций может быть сформулирована как вариационная:

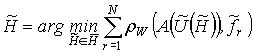, , . (1)

Для придания определенности вектор-функции и выбора пространства , определяющего подмножество решений, входящих в компакт, рассмотрим свойства решений нелинейных краевых задач теории оболочек. Необходимо подчеркнуть, что в такой постановке единственность не предполагается и не требуется – единственный элемент определяется выбранным алгоритмом минимизации [2].

Воровичем И. И. показано [3], что обобщенное решение нелинейной краевой задачи теории оболочек в перемещениях описывается интегральными тождествами в специальных функциональных пространствах.

Если ввести функциональное пространство вектор-функций перемещений , у которых , вектор с нормой:

,

где ; – компоненты деформаций, характеризующие нелинейное деформирование оболочки, тогда метрику для этого пространства можно определить как

, (1)

где – вектор, характеризующий нелинейное НДС оболочки при фиксированном значении вектора параметров ; – компоненты обобщенных деформаций, выраженные через компоненты вектора перемещений ; – вектор наблюдаемых значений обобщенных деформаций. Отсюда следует, что , а для задания функций обобщенных деформаций может быть выбрано пространство , метрика в котором определяется как

.

Вычислительный эксперимент был реализован на примере решения задачи идентификации функции неравномерного распределенного внешнего давления , действующего на цилиндрическую оболочку по области в виде полосы. Оболочка (, , , , – длина, радиус и толщина оболочки соответственно, ) закреплена по торцам. Модель конструкции задавалась в конечно-элементной форме. В данной работе приведено численное построение функционалов (1).

Функция внешнего давления принималась в виде:

,

где – угловая координата; – компоненты вектора параметров . Из решения прямой задачи определено НДС, в узлах конечно-элементной сетки получены значения деформаций в верхнем и нижнем слое конструкции, а также значения перемещений, которые выступают в качестве векторов значений результатов измерений. На рис.1 приведены значения норм , , вычисленные в метриках пространств и соответственно, в зависимости от параметра . Кривые 1–3 описывают изменение , кривые 4–6 – значения для разных значений , где , – собственное значение соответствующей прямой краевой задачи.

Сравнение этих зависимостей показывает, что метрика является нелинейной функцией , в то время как изменяется слабо с ростом .

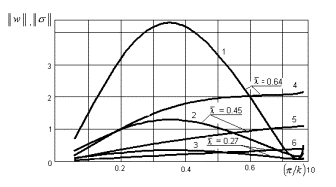
Рис.1 Зависимость значений и от изменяемости нагрузки

Литература:

1. Сергиенко И. В., Дейнека В.С. Системный анализ многокомпонентных распределенных систем – К.: Наук. думка, 2009. – 638 с.

2. Тихонов А. Н., Арсенин В.Я. Методы решения некорректных задач – М.: Наука, 1986. – 286 с.

3. Ворович И. И. Математические проблемы нелинейной теории пологих оболочек – М.: Наука, 1989. – 373 с.