Технические науки/3. Отраслевое машиностроение

А. Ю. Денисов, Ю. В. Денисов

Уральский федеральный университет имени первого Президента России Б.Н.Ельцина, Россия

Статистический анализ температурных напряжений.

Рассматривается использование методов теории вероятностей для определения температурных напряжений в рабочем инструменте прокатных станов и машин непрерывного литья заготовок.

Для определения этих величин анализируется поведение рабочего инструмента в реальных условиях эксплуатации, когда учитывается случайных характер внешних воздействий на инструмент. В этом случае на первый план выступает постановка вероятностной задачи и метод ее решения. В такой интерпретации задача становится актуальной для инженерных расчетов на надежность и для определения срока службы инструмента в вероятностной постановке.

Решается задача линейной термоупругости для бесконечного изотропного цилиндра, механические свойства которого предполагаются детерминированными. Цилиндр нагружен случайной неосесимметричной нагрузкой и находится в нестационарном, неосимметричном случайном температурном поле. Определяются моментные функции (МФ) различных порядков случайных напряжений, деформаций, перемещений и температуры внутри цилиндра.

1. Пусть σ_ij, ε_ij, х_i., τ – случайные напряжения, деформации, перемещения и температура, с_ijmn- тензор постоянных упругости, а_ij – тензор коэффициентов линейного расширения, к – коэффициент температуропроводности. Тогда для статистической модели уравнения краевой задачи несвязанной термоупругости имеют вид:

; , (I)

а температура и напряжения на границе бесконечного цилиндра радиуса R

(2)

Здесь θ –детерминированный угол; γ_n, ε_n, η_n, λ_n, μ_n, υ_n – случайные постоянные с известными статистическими характеристиками.

Под решением системы (1) при условиях (2) подразумевается отыскание МФ различных порядков случайных напряжений, деформаций, перемещений и температуры, удовлетворяющих соответствующим уравнениям и граничным условиям.

2. Определение МФ-1. Введем обозначения <…> - оператор математического ожидания,

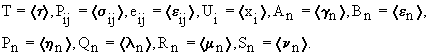(3)

Применив к (1), (2) оператор <…>, получим уравнения для МФ-1, совпадающие с уравнениями классической термоупругости:

(3)

. (4)

Решение уравнения теплопроводности в МФ-1 при нулевых начальных условиях получим, используя преобразование Лапласа^*)

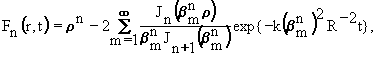(5)

- функция Бесселя порядка n; β_m-положительные корни уравнения .

Задачу термоупругости будем решать в перемещениях. Тогда система (3) при граничных условиях (4) преобразуется к виду

(6)

где λ,μ – коэффициент Ляма; I- объемное расширение.

Решение системы (6) ищем как сумму общего решения однородной системы уравнений и частного решения неоднородной системы. Частное решение находим с помощью термоупругого потенциала перемещений [1] U_i=W_,i , который можно рассматривать как МФ-1 случайного потенциала Ф,W=<Ф>.

Соответствующие термоупругому потенциалу температурные напряжения

Найденные МФ-1 температурных напряжений не удовлетворяют граничным условиям (4). Для их удовлетворения следует сложить полученное решение с решением изотермической задачи теории упругости, которое может быть получено известными методами.

*) Для сокращения записей дальнейшие результаты приведены для В_n=0, Q_n=S_n=R_n=0

Тогда граничным условиям (4) удовлетворяют моменты первого порядка полных напряжений - решение однородной системы (6). Проделав соответствующие вычисления, получим МФ-1 полных напряжений внутри бесконечного цилиндра.

3. Определение МФ-П. Пусть вариации случайных функций

Обозначим корреляционные функции напряжений, деформаций, перемещений температуры и термоупругого потенциала:

корреляционные моменты случайных величин

Тогда система уравнений термоупругости для МФ-П при отсутствии корреляции между напряжениями и температурой примет вид:

(8)

Граничные условия для МФ-П температуры и напряжений:

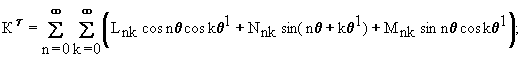
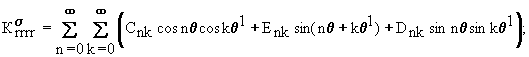(9)

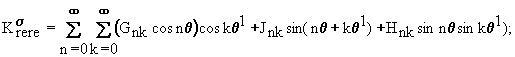
Система уравнений для МФ-П перемещений при граничных условиях (9)

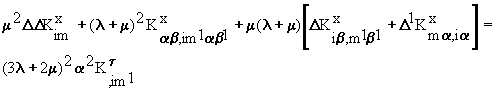(10)

Тогда математическая постановка задачи для моментных функций второго порядка перемещений формулируется следующим образом: необходимо найти шесть функций , удовлетворяющих в области занятой телом, дифференциальным уравнениям (10) и граничным условиям (9). Решение системы (10) можно записать в виде суммы частного интеграла неоднородных уравнений и общего интеграла однородной системы.

Аналогичным образом могут быть получены моментные функции более высоких порядков. Если случайные постоянные распределены по нормальному закону, то случайные температура и напряжения внутри цилиндра также будут распределены по нормальному закону. В этом случае моментные функции первого и второго порядков позволяют вычислить плотности частных распределение случайных напряжений. Эта информация может быть использована для определения показателей надежности.

4. Числовой пример. Пусть температура и напряжения на границе заданы следующим образом:

Статистические характеристики случайных величин: А₀=500⁰; А₁=400⁰;

Р₀=Р₂=-0,5·10⁸нм^-2; L₀₀=L₁₁=75·10² град²; L₀₁=50·10² град²; С₀₀=С₀₂=2·10¹³н²м^-4;

С₀₂=10¹³н²м^-4; принимаем υ=0,35; Е=1,96·10¹⁰нм²; α=11,4·10^-6 град^-1;

к=10^-5м²сек^-1; кR^-2t=0,1.

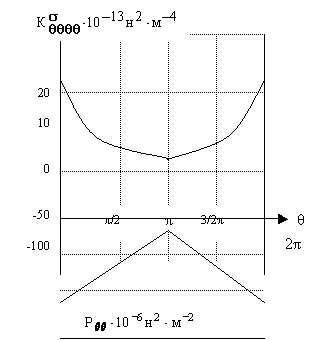
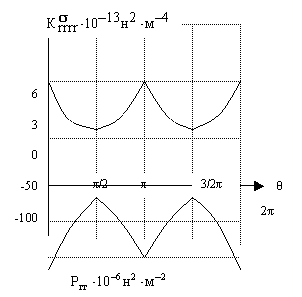
	Рис. 1. Зависимость среднего радиального напряжения и его дисперсия от угла θ.
				Рис.2. Зависимость среднего тангенциального напряжения и его дисперсия от угла θ

На рис.1. и рис.2 приведены моменты первого и второго порядков случайных напряжений при ρ=0,7.

Литература.

1. Паркус Г. Неустановившиеся температурные напряжения. Физматгиз, 1963.